①ルートの中身を簡単にする 分数を書くときは \(\dfrac{6}{4}=\dfrac{3}{2}\) のように可能な限り「約分」をしますよね。 それと同じで、平方根を使って数を表すときは ルートの中身を可能な限り小さな自然数 にします。 ルートの計算で分数の分母を有理化しないといけない理由とは? 中学校の数学で、分母にルートがついた数があることを嫌います。 と、言うよりもやっちゃダメという感じですよね。 高校生になると一部分母にあってもいい感じにはなりますが、中学校Step 3 部分分数分解(以下を参照)の適切な形に書き下し、たすき掛けをして定数を求める。 Q ( x ) {\displaystyle Q(x)} については、1次因数( a x b {\displaystyle axb} の形)と既約の2次因数( b 2 − 4 a c < 0 {\displaystyle b^{2}4ac
1
分母に分数 ルート
分母に分数 ルート-分母に変数がある問題は相加相乗平均を使って解くことが圧倒的に多いです。 ことが多いんだったんだよね。でも、今回の問題は\(\frac{x}{x^2x1}\)と分数に変数を含んだ関数です。 ルート(1039)ってどうやったら簡単にルートを外せますか?※ 分母は「なるべく」正の数になるようにします.(高校以上では様々な場面で,分母を負の数のまま使うこともありますが,中学校の基本の段階では,「分母は正の数にする」ように決める方がよい.) ※ 上の式で,分母と分子を −2 で割ると,それぞれ符号が変わりますので




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題
「ルートの内側の数字同士は割る事が出来る」ことを思い出しましたか? つまり、 分数の割り算も、分母・分子は割ることが出来ましたね、それと一緒です。 この計算が出来れば、ルートの割り算は80%理解できたも同然です、ご安心ください。 分数というのは、分母と分子の両方に同じ数を掛けるのであれば 大きさは変わらないという特徴があったよね! だから、分母と分子の両方に同じルートを掛けることで 分数の大きさを変えることなく 見た目だけをチェンジすることができるってわけ!分母に分数を含む式 ここでは、分母に分数を含む式の計算のしかたについてみていきましょう。 次の式を簡単にしなさい 難しい分数式を考える前に、簡単な分数を例に考えてみましょう。 この分数式について考えてみます。
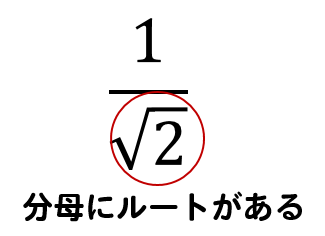
普通は「分母を有理化(ルートをなくす)」して、分母にはルートがない形にします。 2/√ (5/3) = 2√3 /√5 平方根 (分母の有理化) 中3数学 分数の上下に同じ数字を掛けて、分母のルートを外す作業です。 ルートの計算がしっかり定着していれば決して難しくはないですが、約分やルートを簡単にできるときは必ずすることだけは注意しましょう。分母にルートがある分数を、分母にルートがない分数に変換することを 有理化 (ゆうりか)と言います。 1 3
分母の有理化 第11回 有理化することとは、無理数から有理数を作るこ とです。特に分数の場合、分母に√(ルート)を含 =1÷ 2 (分数は、分数や小数の場合はどうやる?←今回の記事 平方根、ルートの値を語呂合わせ!覚え方まとめ a√bの形に変形するやり方とは? 平方根の大小関係を不等号で表す問題を解説! 根号を含む式の値の求め方とは? 分母の有理化のやり方はこれでバッチリ! 分母を有理化したりで忙しいからね。 ルートの分数の計算なんて解きたくないぜ。 今日はそんなちょっとやっかいな、 ルート分数の割り算の計算方法 を4ステップで解説していくよ。 よかったら参考にしてみて^^ 平方根の分数の割り算の解き方の4ステップ




Plumbago 雑記 数学 分数の分母 分子どっちが虚数かで結果が変わるってマジ 平方根 分数 虚数



1
数学・算数 分母、分子が分数になる時 3分の2分の 4分の3とか ルート2分の1分の ルート2分の1とか このようなことが起こりうるものでしょうか? もし分数がさらに分数になってしまうようなと 質問No 「 分母を(a b)(a −b) = a2 −b2 (a b) (a − b) = a 2 − b 2 の形にする 」というお決まりのパターンで解けるので、一度覚えてしまえばもう安心です。分数のなかに分数が含まれる計算の解説プリント 分数の中に分数が含まれる計算の解説 分数の中に分数が含まれるものの解法については主に2種類あります。 まず、ひとつめの割り算を使う解法です。 \(\frac{b}{a}=b\div a\)なんだよね。



1




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題
ルートxを含む式の積分公式 具体例で学ぶ数学 > 微積分 > ルートxを含む式の積分公式 最終更新日 ∫ x d x = 2 3 x 3 2 C ∫ 1 x d x = 2 x C 目次 ルートxの積分 置換積分を用いる方法 分母にルートがある式の積分ルートを含んだ極限を考える際、注意すべき点は次の2点です。 ポイント そのまま極限を考えると\(\infty \infty, \frac{0}{0}\)不定形になる場合、有理化を使うとうまくいく場合が多い。 「g / b」の場合、「g」が分子、「b」が分母となります。 分数と言っても、数学の様に「g」を「b」で"割る"訳ではありません。 このような分数コード表記は、「分子のコードのルート音とは違う音をハーモニーの最低音に指定する」時に使用されます。



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典



高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド
分母の有理化の方法(ルートn) 分母が n \sqrt{n} n である分数は,分母と分子に n \sqrt{n} n をかけることで有理化できます。 (ただし n n n は整数とします) ただそうすると、分母に $(u1)\sqrt{u}$ が残ってしまい、計算するのが難しくなります。 ここで $\sqrt{u}$ を別の文字で置くなら、はじめから $\sqrt{x^21}$ を別の文字で置く、上のやり方をやったほうがいい、ということになります。 数学 分母にルートの分数がある場合の計算方法が分かりません。 写真のような答えになる過程を教えて欲しいです! どなたか分かる方いらっしゃいますか?? 数学 6 √8 (ルート8分の六)の分母を有理化して下さい!




ルートの計算で分数の分母を有理化しないといけない理由とは さびねこ中学校




平方根 ルート の重要な計算方法まとめ 数学fun
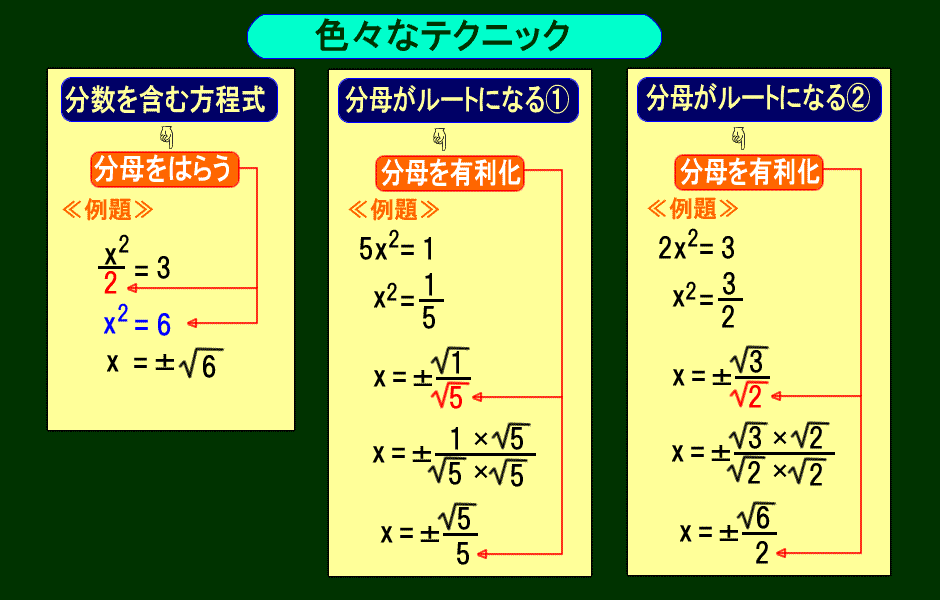
となって, x3i=4yi が成り立ちます. *) 要するに, x, y が実数という条件がなければ, x3i=4yi を満たす複素数 x, y は幾らでもあります. 問題3 次の等式を満たす実数 x, y を求めてください. (右の選択肢から選んでください) (1) x4i=5yi 実部の 分数の分母 や分子に分数 この記事では, 2 \sqrt{2} 2 以外の「ルート」について連分数でどのように表すか考えてみます。面倒くさがらずに,紙に描きながら数式を追ってみてくださ分母の有理化1 分数の分母に平方根がある場合に分母の平方根をなくすことを 有理化 という。 解説動画 ≫ 分母を有理化せよ。 5 3 7 8 9 5 12 ① 5× 3 3 × 3 = 5 3 3 a × a =aという性質を利用して、 分母にある√と同じ√を 分母、分子にかける。



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス
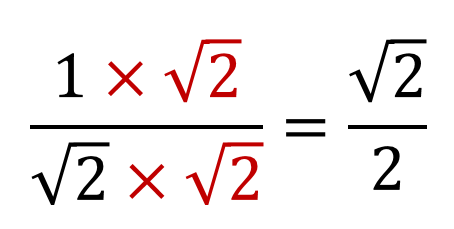



平方根 分母の有理化のやり方はこれでバッチリ 数スタ
<かず子> まず(1)ね.分母をみると,x=0とx=1の2個所に穴が空いてるわ. <よしお>でも,x→0だから,x=0の穴埋めをすれば十分.そのためには, これで穴が埋まった.そして,x→0とすれば,穴埋めした関数にx=0を代入してやると, となります. <かず子>では(2)ね.でもこれは,どこに穴3 ルートの微分まとめ 1 ルートの微分の求め方 結論から言うと、ルートの微分は、 べき乗の微分公式 を使うと簡単に求めることができます。 なぜなら、以下で示している通り、ルートとはべき指数が分数のべき乗だからです。 ルートはべき指数が分数 分母に2つ項がある場合には この乗法公式の性質を利用して進めていきましょう。 分母にある に対して 1つの項の符号を変えた の式を分母分子にかけていきます。 かず先生 ちょっと計算は複雑になっちゃうけど やってることはシンプルだよね 分母に



根号計算 約分




ルートの値を代入する問題 色んな知識を使う良い問題です 中学や高校の数学の計算問題
冒頭のように、分母にルートがある分数を変形して、分母にルートがないようにすることを「有理化」と言います。 例えば、$\dfrac{2}{\sqrt{3}}$ を考えてみましょう。「2乗するとルートが消える」ので、分母分子に $\sqrt{3}$ を掛ければいいですね。 ルート分数の掛け算は3ステップでとけちゃうよ。 分母の有理化 約分 分母・分子同士をかける Step1 分母を有理化する 分母を有理化しよう。 答えは有理化しなきゃいけないから、先にやっちまうのがベストだ。 ⇒ 分母の有理化の方法 はこちら




複素数の分数の実数化 分母の有理化の複素数版 Irohabook




高校数学 繁分数式 分数の分数 の計算 受験の月
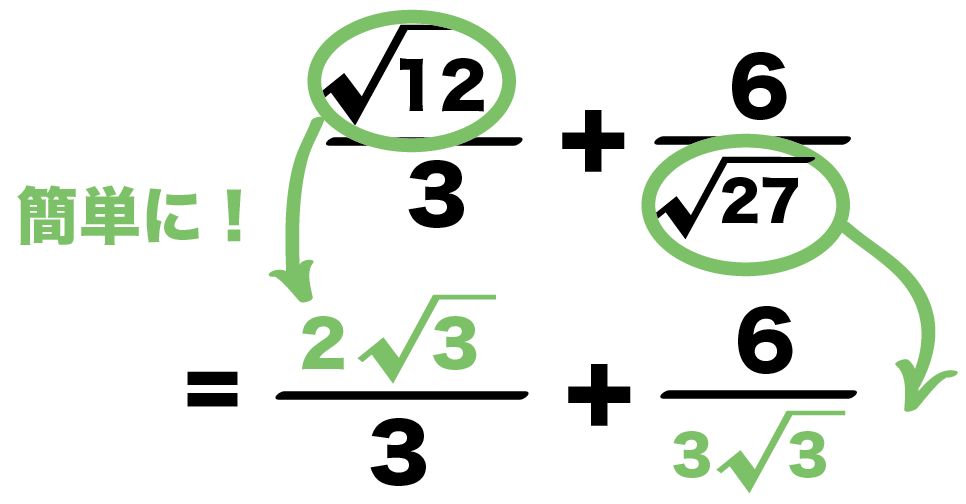



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




2の平方根 Wikipedia




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




中学数学 平方根 のコツ 有理化 加減乗除 展開



ルート の分数計算教えてください すみません 急ぎです Yahoo 知恵袋




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ



Math 超簡単 有理化 分母に根号がない形にする 働きアリ



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ




分数を有理化しよう 分母にルートが2つある時はどうしたらいいの さびねこ中学校
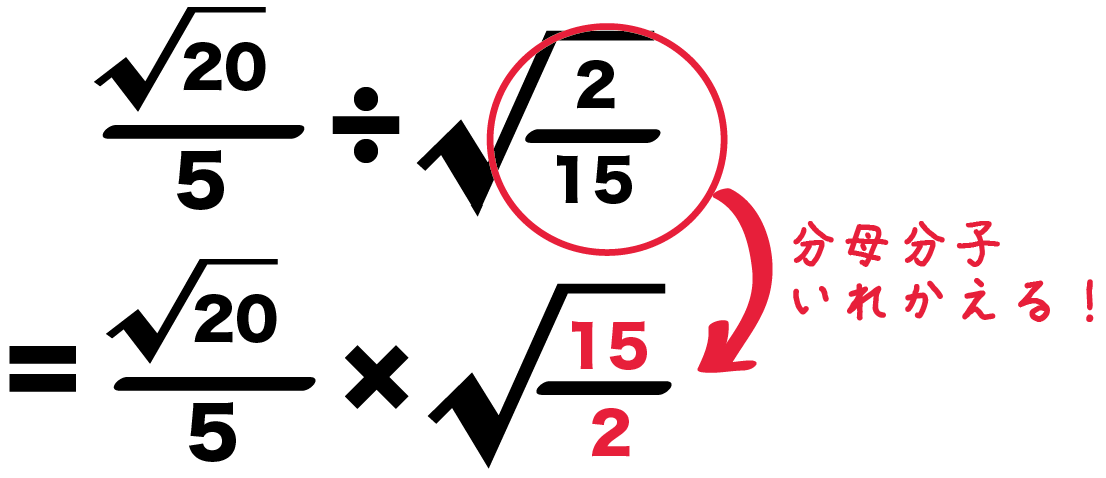



平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学
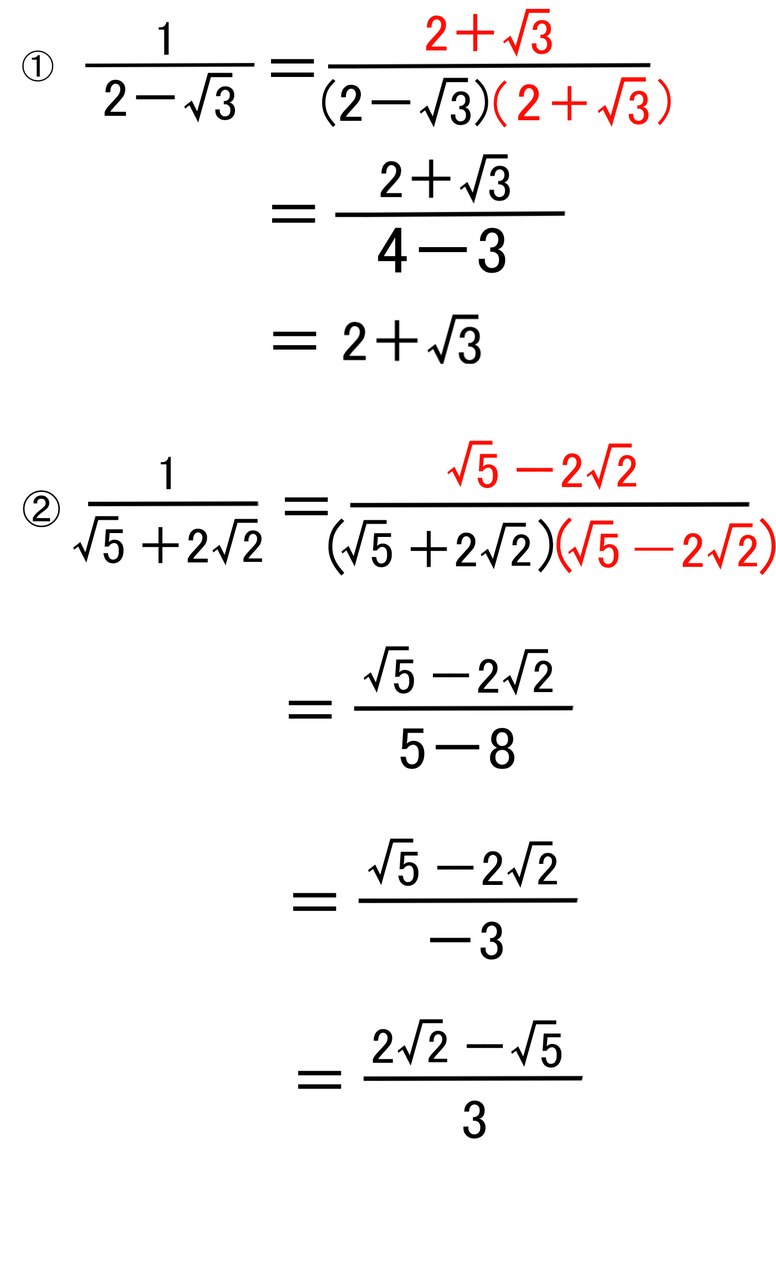



平方根 5 分母の有理化 バカでもわかる 中学数学




高卒認定試験数学の平方根 分母の有理化の解き方を解説 坂田先生のブログ



中学3年 数学 2次方程式 解き方 平方根の利用 有理化あり 問題1




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo




数学の質問です 分数関数の分母に二乗がついていた場合はどのように計 数学 教えて Goo




愛されし者 ルート 計算 足し算
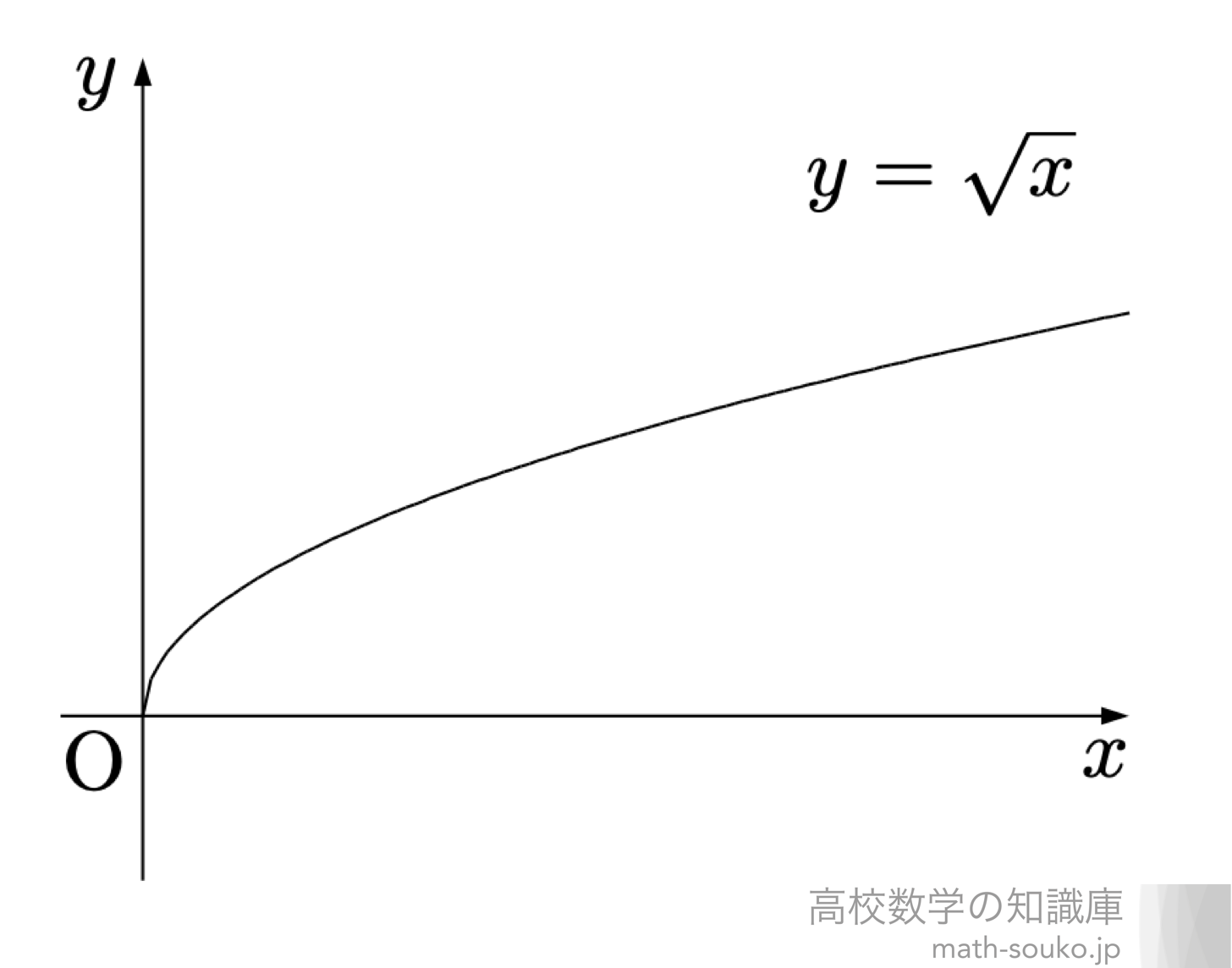



無理関数とは 定義域とグラフ 高校数学の知識庫




根号をふくむ足し算と引き算 の分数をふくむ場合 Youtube




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




分母の有理化 Youtube




2つの解法 3乗根の有理化 数学ii 指数関数と対数関数 Youtube




ルート分数の有理化 項2つ3つある場合は やり方まとめ 高校生 中学数学 理科の学習まとめサイト




有理化の分数計算 看護受験の必須 数学の公式を確認テスト Vol12 Kazアカデミー 大阪の看護学校 看護予備校




部分分数分解の公式 やり方と分数数列の和の求め方 理系ラボ
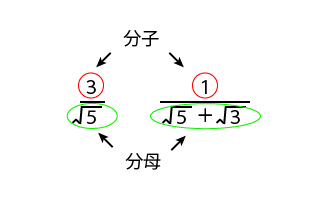



有理化 もう一度やり直しの算数 数学




数学のルートの分数の二乗 この式の計算方法を教えてください Okwave




部分分数分解の公式 やり方と分数数列の和の求め方 理系ラボ




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo




平方根 ルート の重要な計算方法まとめ 数学fun




ルートの分数計算 問題解説で完全マスターだ 数スタ




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




複雑な分母の有理化 Youtube




有理化の計算 やり方は 分母のルートを分子にかけるだけ 中学や高校の数学の計算問題



分母にルートが使われている分数が入った計算方法がさっぱり分かりません Yahoo 知恵袋




バカでもわかる 中学数学 平方根



分数関数の不定積分



分数の分母が分数であり その分母がルートの場合の計算の仕方がよくわかり Yahoo 知恵袋




部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス
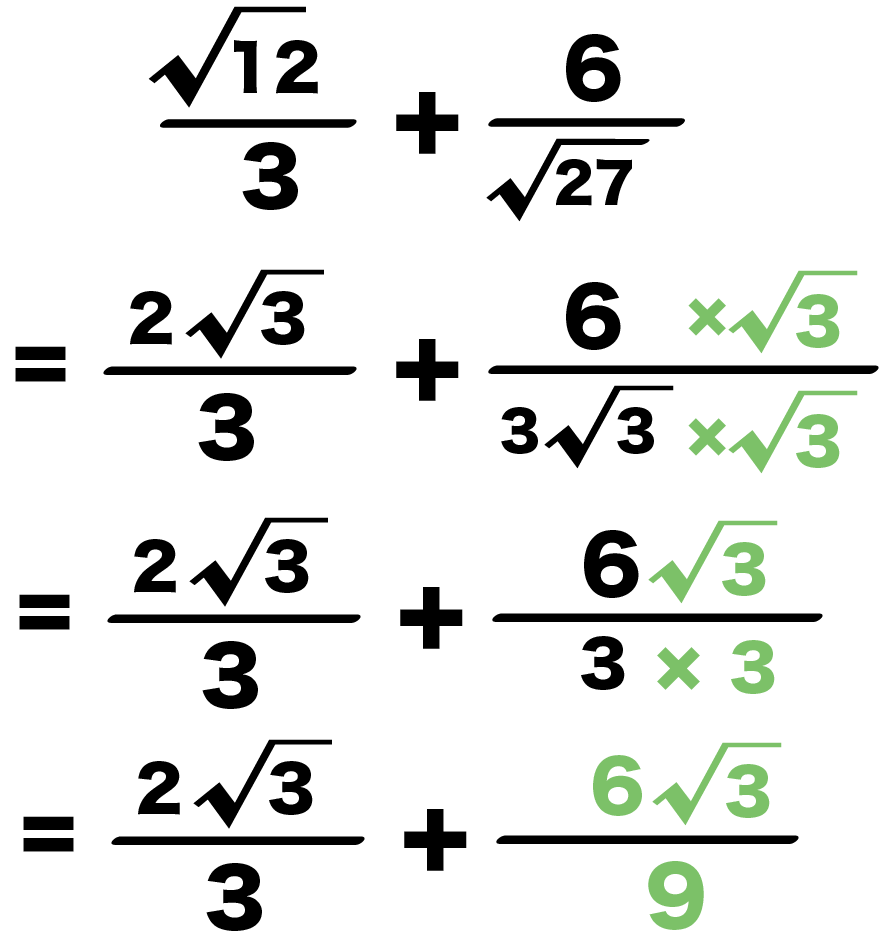



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



分子と分母にルートがある分数式の変形 途中の分数の変形が何故こう Yahoo 知恵袋




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
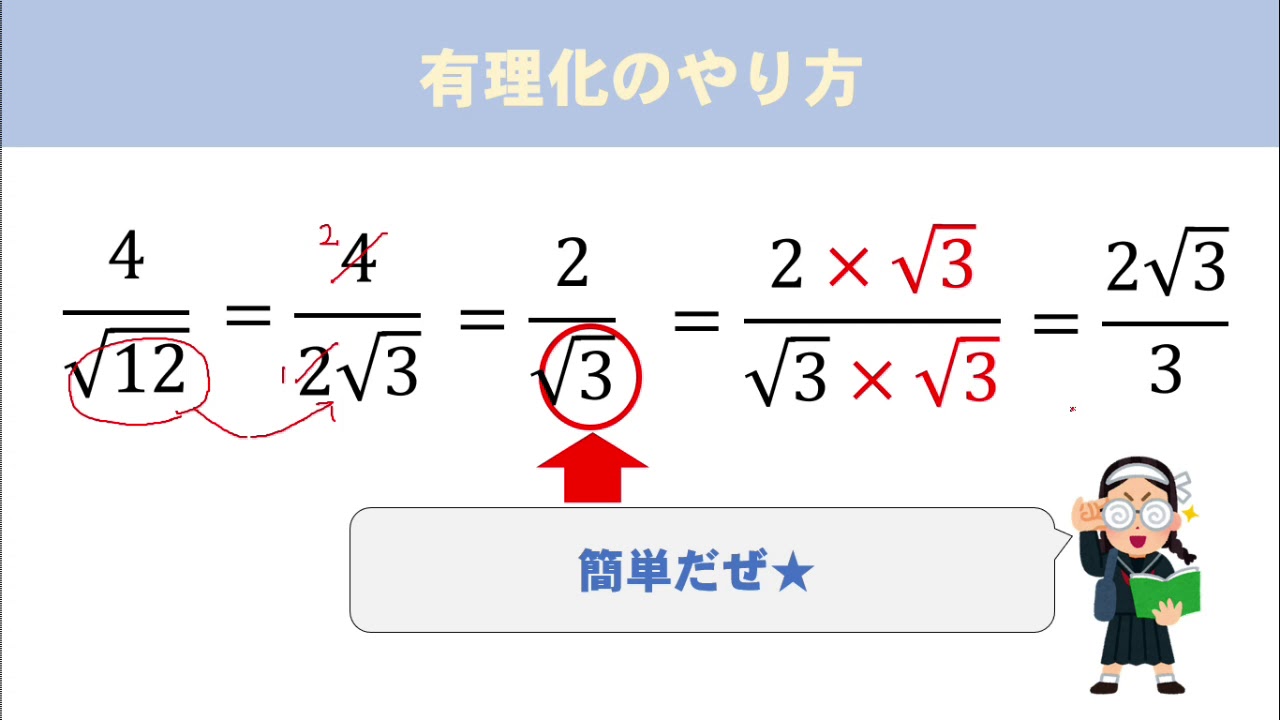



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




三項の有理化 高校数学 Youtube




中学数学 平方根 のコツ 有理化 加減乗除 展開




これで完璧 平方根の基礎 中3数学 中学生の勉強法




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




平方根 ルート の計算をおぼえよう しろカスと学ぶ中学数学 理科
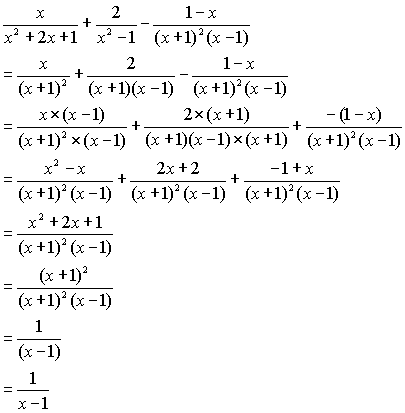



分数の復習と分数式の計算




平方根 ルート の重要な計算方法まとめ 数学fun




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




分母の有理化の方法 数学の偏差値を上げて合格を目指す
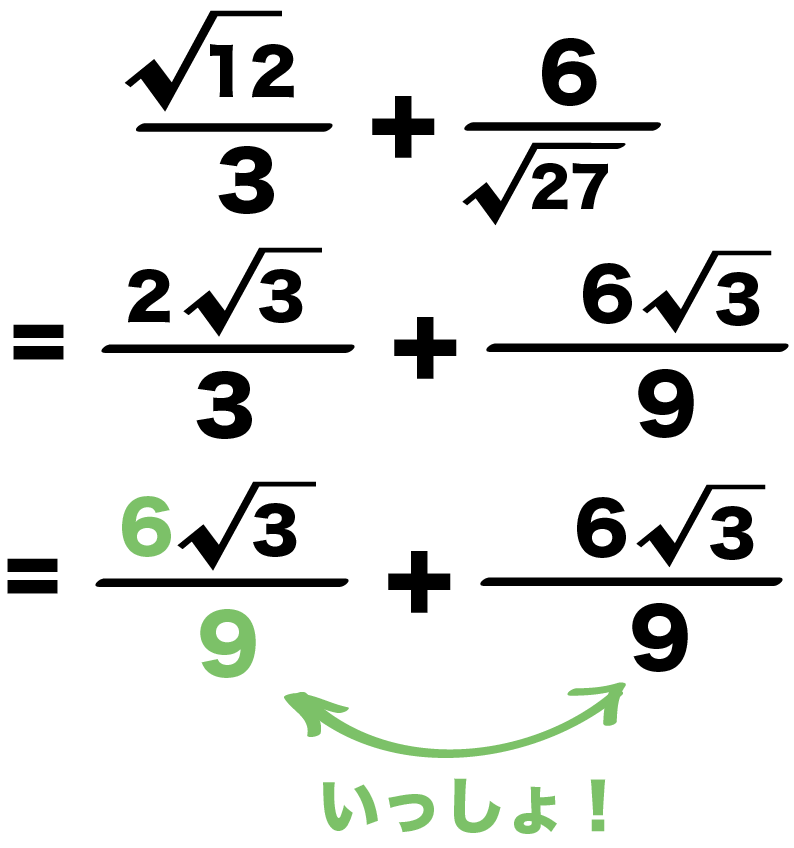



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




割り算をしたとき その数は分母と分子のどっちに行くか覚えよう 中学や高校の数学の計算問題




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題
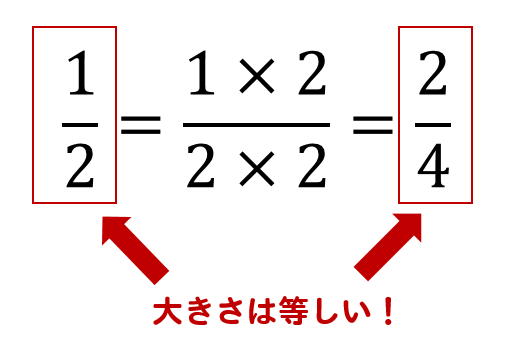



平方根 分母の有理化のやり方はこれでバッチリ 数スタ
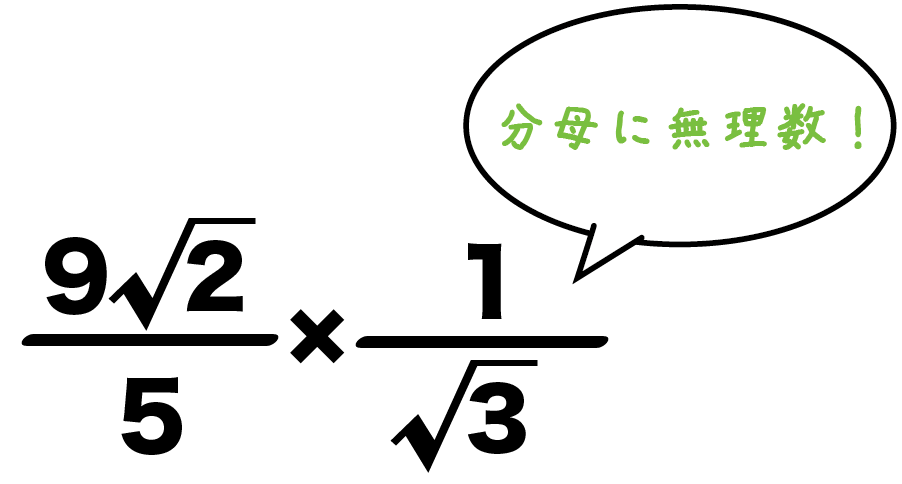



ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




数学のルートの分数の二乗 この式の計算方法を教えてください 数学 教えて Goo
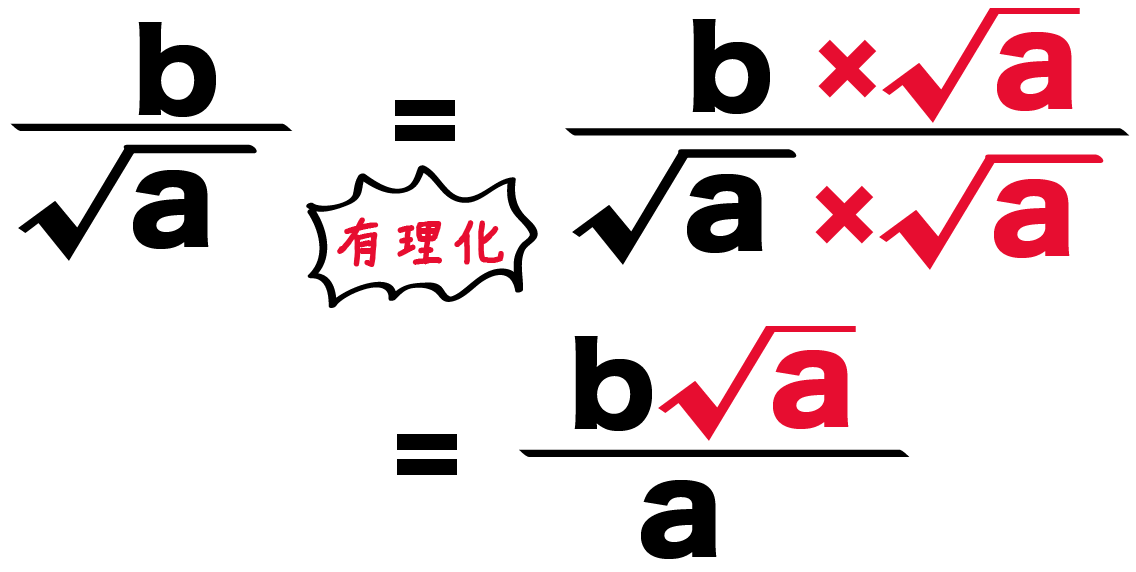



平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




実数 ルート を有理化する意味はこれでわかる 分母に がngの巻 Vol 9 3回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校



分数の分母が分数であり その分母がルートの場合の計算の仕方がよくわかり Yahoo 知恵袋



この分数分の分数 の計算の仕方がさっぱりわかりません ルートがあるから余 Yahoo 知恵袋
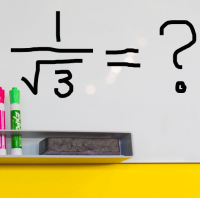



平方根 分母の根号 ルート をなくす 有理化 苦手な数学を簡単に



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係




平方根 ルート の重要な計算方法まとめ 数学fun




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




ルートの中を簡単にする と 分母の有理化 を比べる とちぎeライブラリ




数学のルートの分数の二乗 この式の計算方法を教えてください 数学 教えて Goo



1



根号計算 約分




ルートの入った計算なのですが この場合って分母に2をかけて分母を消してはダメですよね Clear




練習問題 3分でできる ルート分数の足し算 引き算 Qikeru 学びを楽しくわかりやすく
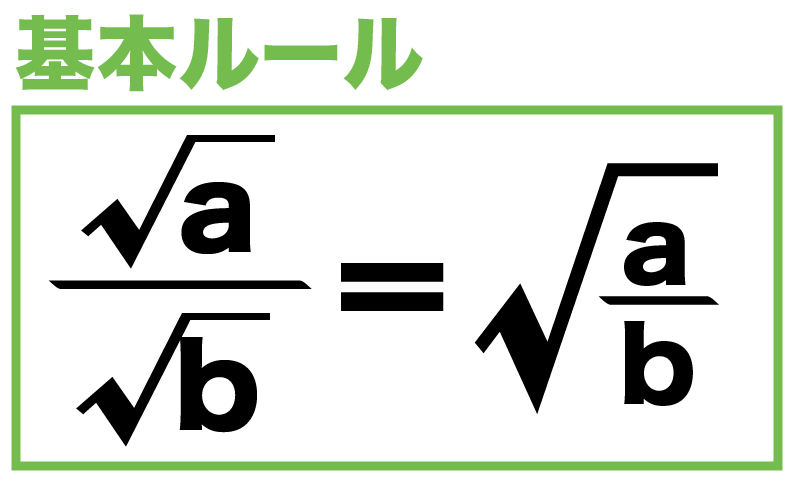



平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく




ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



分数の2乗とは 1分でわかる意味 計算 書き方 との関係




答えが分数のとき 分母にルートがあったら消す のように分母がマイナスのときはプラスに Clear




小数や分数のルートの外し方 分数の の外し方は知っておくべきだ 中学や高校の数学の計算問題




複雑なルートの分数の有理化のやり方と問題 理系ラボ




高校数学 数列の極限 無理式の極限 受験の月




部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学



分数分の分数の計算にルートが入った計算がさっぱりわかりません Yahoo 知恵袋




2倍時短 分母の有理化の無駄を省けば計算スピードに差が付く 超わかる中学数学 Youtube



1



0 件のコメント:
コメントを投稿