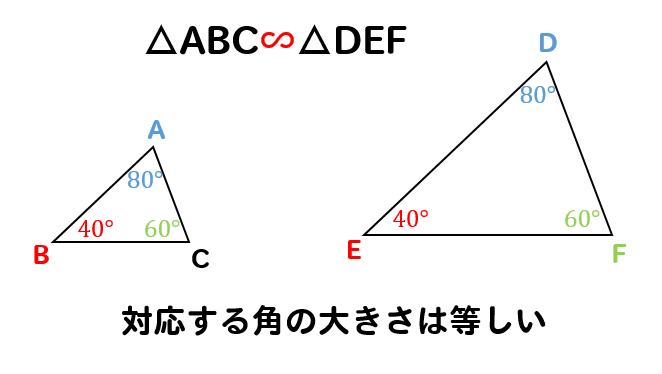
相似な図形の性質 相似な図形というのは 拡大、縮小の関係にある図形のことだと分かりましたね。 それでは、拡大縮小という特徴を押さえつつ 相似である図形には、どんな性質があるのか見ていきましょう! 対応する辺の長さの比は、すべて等しい 相似の位置 定義 相似の位置 :2つの相似な図形において,対応する点を通る直線が全て1点 O O を通り,点 O O から対応する点までの距離の比がすべて等しくなるような位置関係 相似の中心 :相似の位置における点 O O指導案データベースの新着 指導案データベースについて 学習指導案(ひな形) 検索 キーワード一覧 全19件 (1~10件) 分類 単元・題材名 単元・題材ダウンロードファイル

数学 相似の定理まとめ 中学生 数学のノート Clear
相似な図形 条件
相似な図形 条件-これに対し,合同な図形は,形も大きさも同じ図形でした。 ※ 相似な図形の,対応する部分 (辺や半径,弧)の長さの比を「 相似比 」という。図形・相似 中学数学相似とは何か・導入 中学数学三角形の相似条件 中学数学相似の証明・その1 中学数学相似の証明・その2 中学数学相似の重要形 ピラミッド型と砂時計型 中学数学平行線と線分の比・その1




B Bar8cm C E Bar10cm G Lihat Cara Penyelesaian Di Qanda
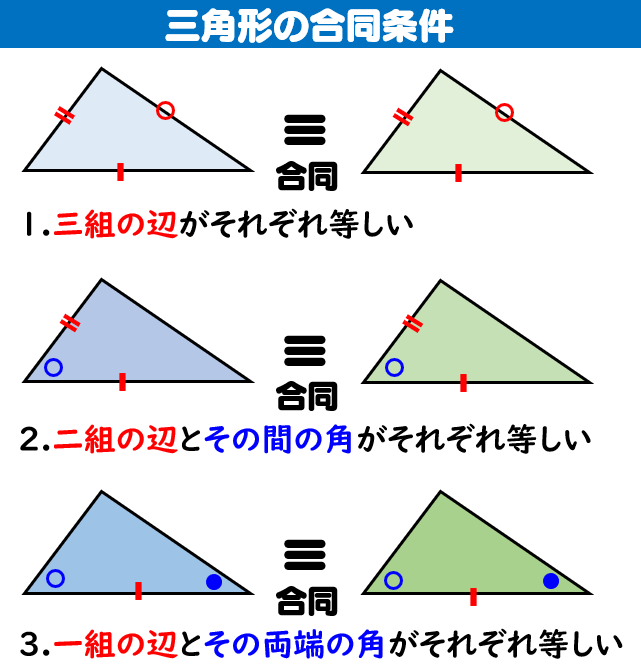
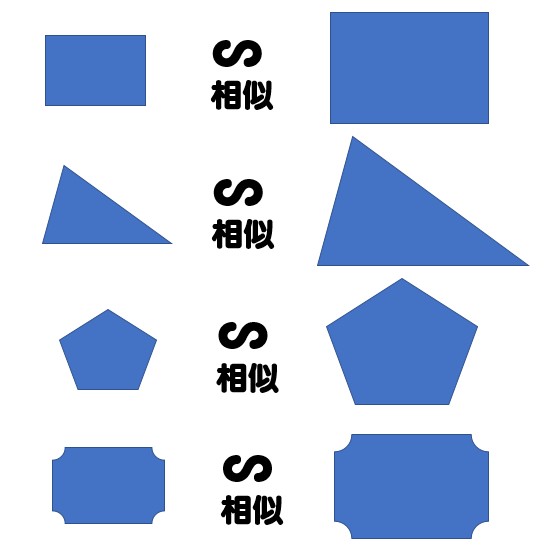
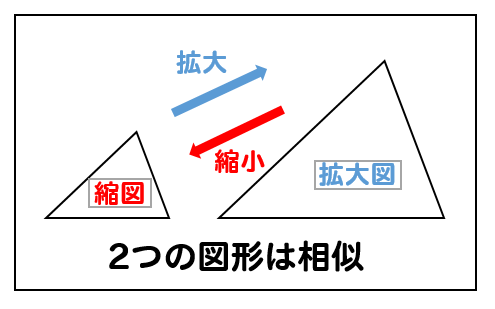
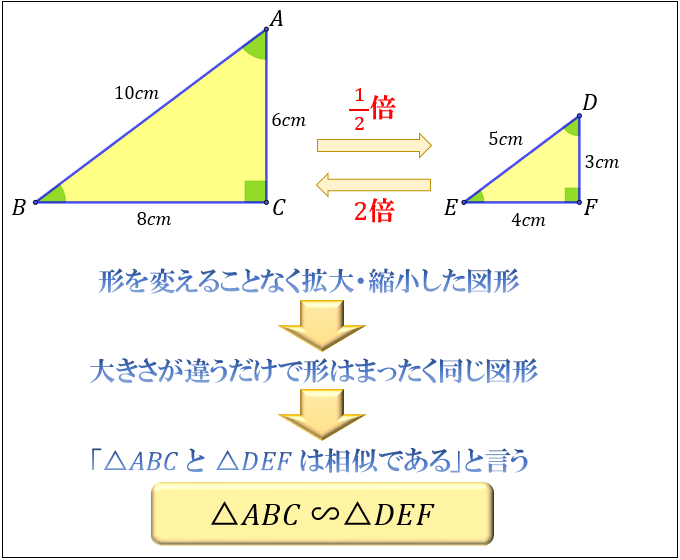
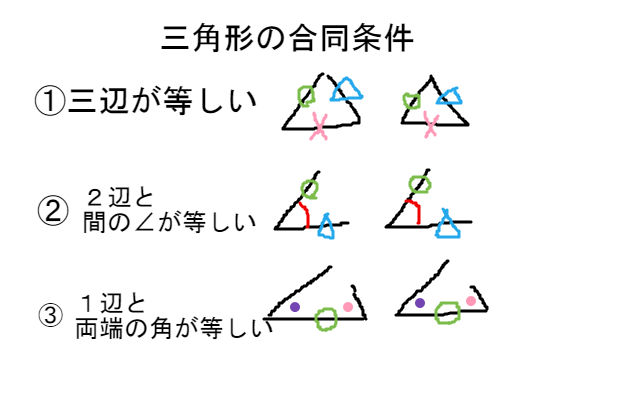
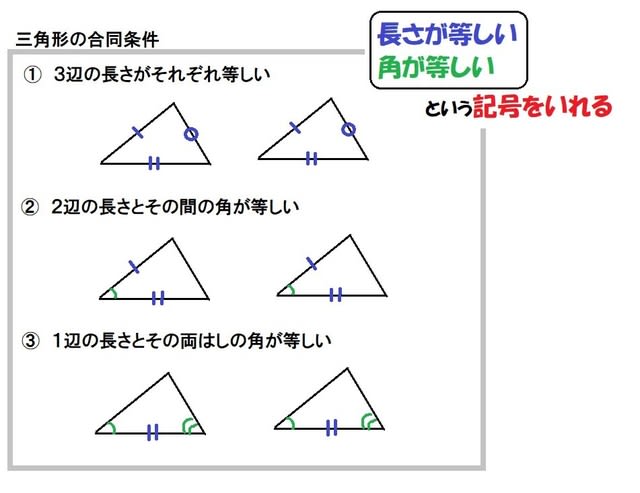
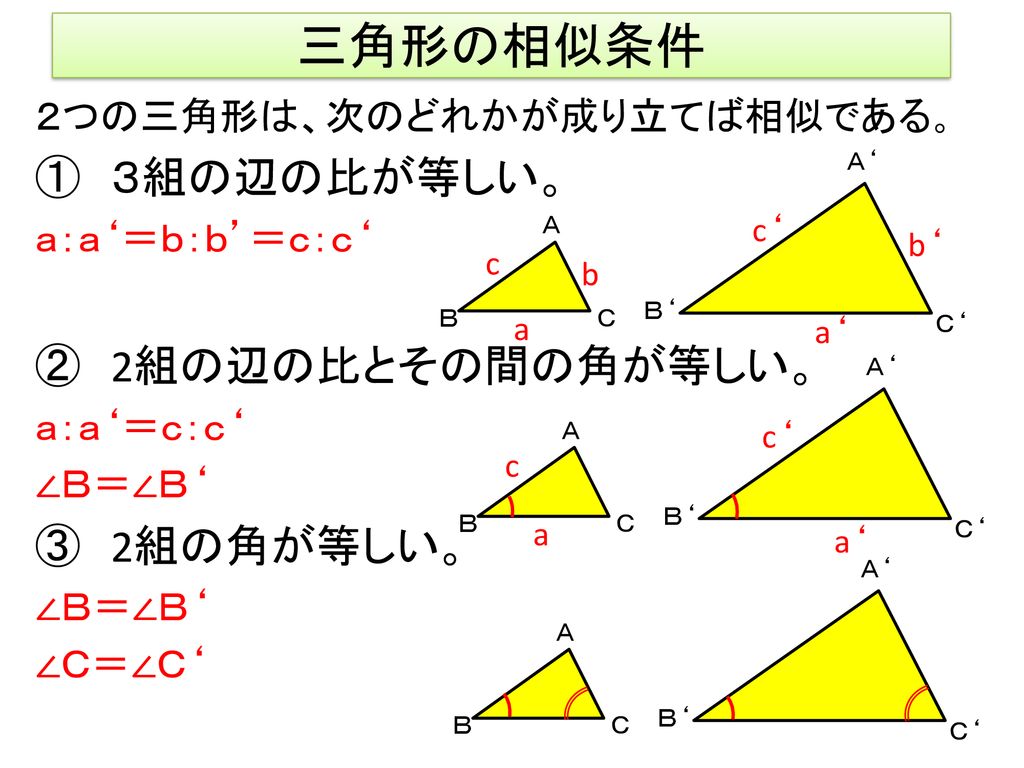
三角形の相似条件 「 三角形の合同条件 」は、「 形 」も「 大きさ 」も同じというための条件。 中3数学図形と相似相似な図形と証明(1~9)のプリント集です。 相似な図形 相似な図形の性質を用いて角度の大きさや線分の長さを求める 三角形の相似条件 相似な図形の証明 相似な図形の証明の応用問題 問題・解答解説付きです。 「同じ形のまま拡大・縮小した図形である」ことを、 相似 と言います。 たとえば、下図の三角形 D E F は「三角形 A B C の形を変えることなく 1 2 倍に縮小した図形」です。
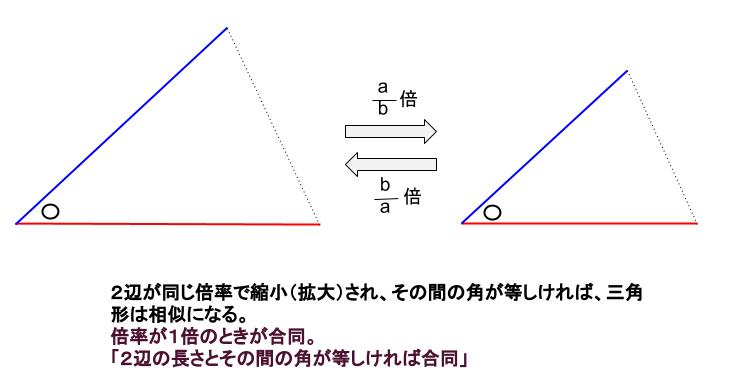
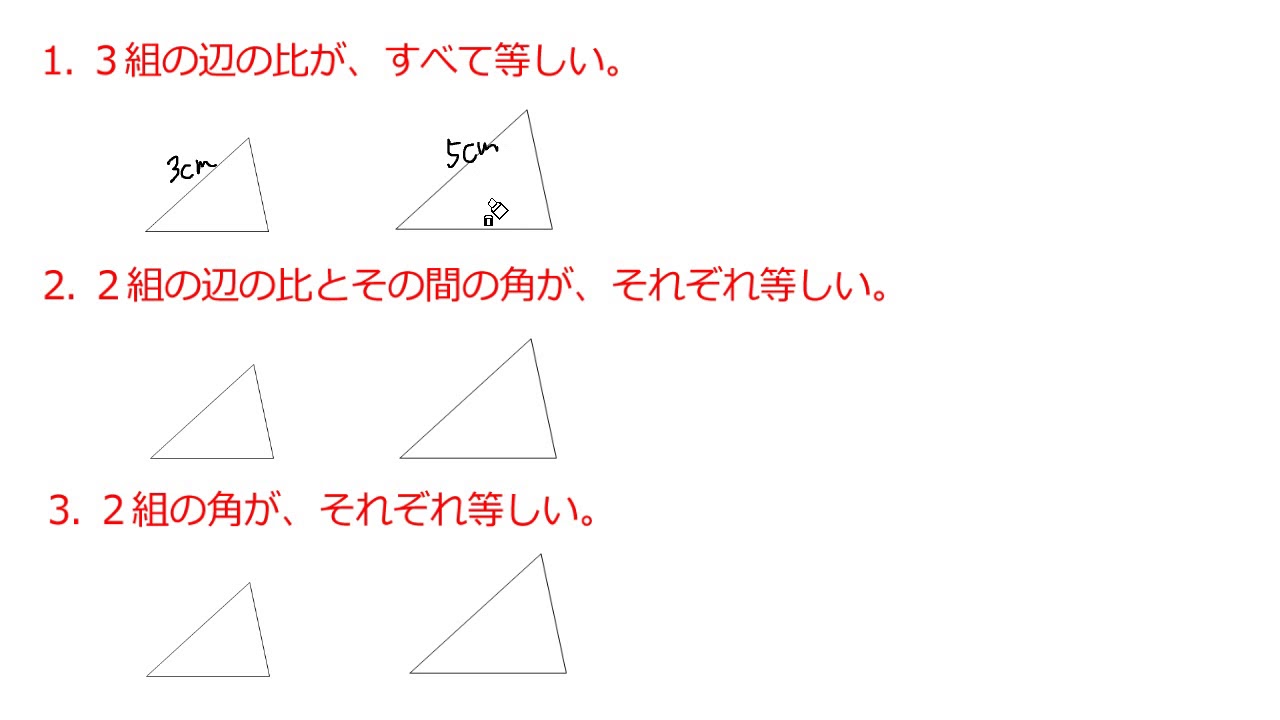
相似条件を満たすとなぜ相似なのか?を考えてみる まずは、三角形の相似条件についての復習 まずは、"相似"についての復習です。 "相似"とは、簡単に言えば、2つの図形の 形 が等しいことをいいます。 三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは 三角形の相似条件 三角形が相似な図形になるときの条件を見ていきましょう。 ・3組の辺の比がすべて等しい ・2組の辺の比とその間の角がそれぞれ等しい ・2つの角が等しい どんな条件か1つずつ見ていきましょう。
相似条件は3つとも必ず暗記するようにしてください! ※「相似」とは、形を変えずに拡大縮小した図形のことです。つまり、三角形の相似条件とは、「2つの三角形の形が全く同じになるための条件」ということです。 相似条件① 相似条件の1つ目は、相似条件2が成立する →(三平方の定理より)残り1組の辺の比も等しい →一般の三角形の相似条件「3つの辺の比がそれぞれ等しい三角形は相似」が使える 次回は 直角二等辺三角形の辺の長さの求め方三角形の相似条件 とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。



三角形の相似条件について 図解で分かる相似条件 アタリマエ



高校入試 英語 数学 図形と相似 相似の基礎
中学校3年 相似な図形 1/21時間(東京書籍:新しい数学3 P112,113) 相似な図形の学習への興味・関心を高めよう ねらい ・写真に写っているものを手がかりに縮尺を求め,それを基に実際の長さ中学数学 相似な図形の内容 z 相似な図形の性質 z 相似の位置 z 相似比 z比の値 z 三角形の相似条件 z 三角形の相似条件を使った証明 z 相似の利用(測量) z 三角形と比 z 三角形と比の定理の逆 z 中点連結定理 z 平行線と比 z 三角形の角の二等分線と比相似比 相似な図形で、対応する線分の長さの比を相似比(そうじひ)といいます。 三角形の相似条件 2年生では三角形が合同になる条件を考えました。ここでは三角形が相似になる条件を考えてみましょう。 三角形の相似条件は、次のようになる。




中学数学 相似の証明問題の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中3数学 三角形の相似条件1 3辺の比 映像授業のtry It トライイット
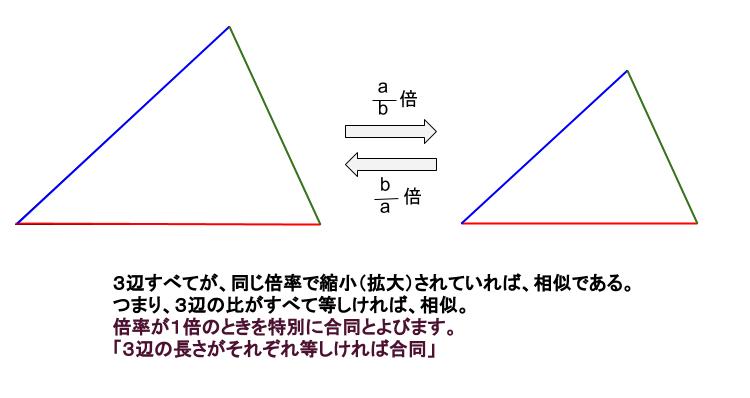
や三角形の相似条件を用いて証明する。(7) 理したことの間のつながりを考える。 ・証明としての形式的な表現等にとらわ 第三次 相似な図形の相似比と面積比及び体積比と れず,日常言語に近い形で確認するよ それらの関係について考える。(2) うにする。1 つの図形を,形を変えずに拡大または( ① )して得られる図形はもとの図形と相似であ るという。相似な図形では,( ② )する角はそれぞれ等しく,(②)する線分の長さの比はす べて等しい。また,線分の長さの比を( ③ )という。(③) 相似な図形では、 対応するすべての線分が同じ倍率で拡大・縮小 されています。 つまり、辺 が辺 の 倍の長さであれば、辺 も辺 の同じく 倍になるということです。




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




相似と相似の条件を知ろう 数学の要点まとめ 練習問題一覧
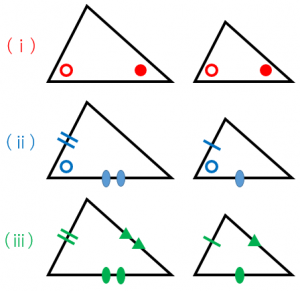
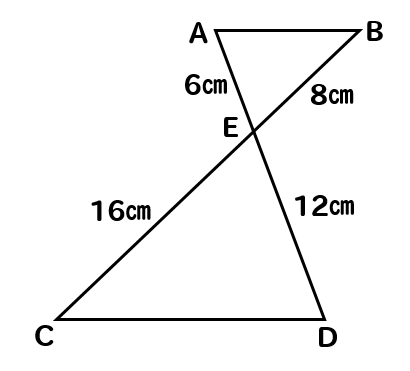
具体例で学ぶ数学 > 図形 > 三角形の相似条件と有名な例題3問 最終更新日 2つの三角形が相似である条件 (i) 2組の角がそれぞれ等しい (ii) 2組の辺の比とその間の角がそれぞれ等しい (iii) 3組の辺の比がすべて等しい 三角形の相似条件を使う例としQ:「相似の位置」,「相似の中心」は 指導しなくてもよいのでしょうか。 a:「相似」は「合同」とちがって,直観的には認識しにくい図形の関係です。そこで,導入の際には,2つの三角 形を必ず並べて置く(相似の位置に置く)ようにしています。




中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ



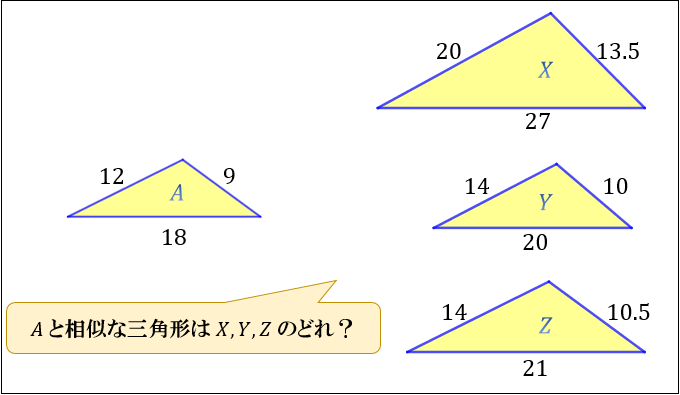
相似な図形 相似条件の練習問題 苦手な数学を簡単に



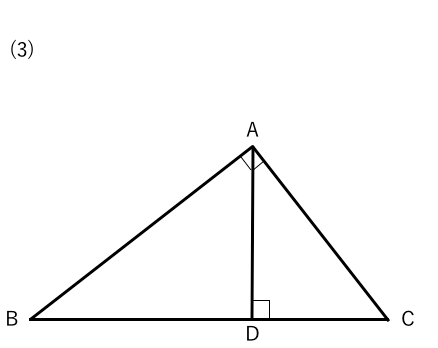
中学数学 三角形の相似条件 中学数学の無料オンライン学習サイトchu Su



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




相似が全くわからないです 分かる方教えて頂けたら嬉しいです Clear




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




中学数学 図形の相似




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
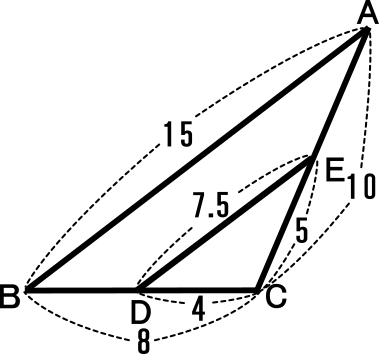



中学3年数学練習問題 三角形の相似条件と証明の問題



三角形の相似条件と証明問題の解き方 数学fun
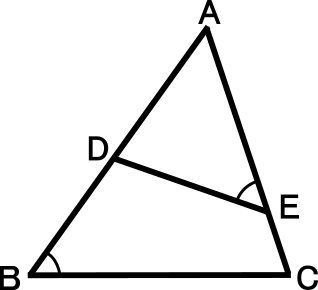



中学3年数学練習問題 三角形の相似条件と証明の問題




2 dgem2 70b603 Descubre Como Resolverlo En Qanda



三角形の相似条件と有名な例題3問 具体例で学ぶ数学
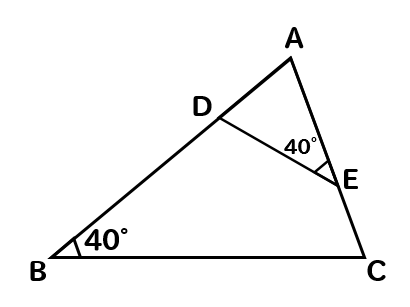



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ




無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明




三角形の相似条件



三角形の相似条件と証明問題の解き方 数学fun




三角形の相似条件




相似な図形 Ict教材eboard イーボード




図形の相似 の問題のわからないを5分で解決 映像授業のtry It トライイット




相似と相似の条件を知ろう 数学の要点まとめ 練習問題一覧




Nitter



1



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ




数学 相似の定理まとめ 中学生 数学のノート Clear



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ




中3数学 相似の証明問題 練習編 映像授業のtry It トライイット



中学数学到達度テスト集中3後期 相似な図形 円 三平方の定理 図形と計量 Gakurin1346 学林舎 通販 Yahoo ショッピング




三角形の相似条件



中3数学 相似の基本性質をわかりやすく問題解説 数スタ
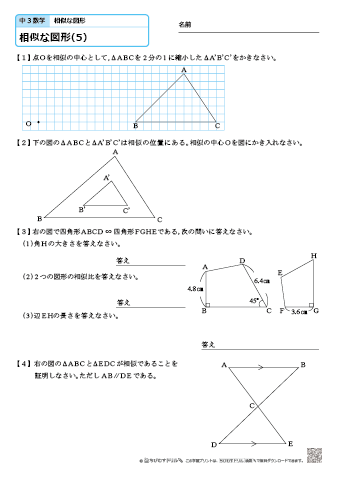



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学 図形と相似9 相似条件と証明 折り返しの図形 すべて無料 星組の中学数学講座



Http Www Fdtext Com Dat Suub3 5zukei 1souji Pdf



高校入試 英語 数学 図形と相似 相似の基礎




Ppt 相似条件と証明 Powerpoint Presentation Free Download Id




至急 この問題の相似な三角形と相似条件を教えてください 考え方が分かりません Clear




相似な図形 三角形の相似条件 中学数学 By となりがトトロ マナペディア
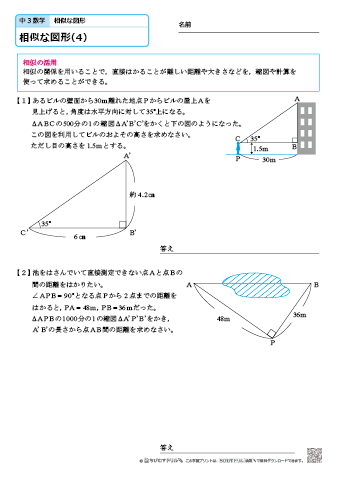



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




B Bar8cm C E Bar10cm G Lihat Cara Penyelesaian Di Qanda




相似な図形 三角形の相似条件 中学数学 By となりがトトロ マナペディア
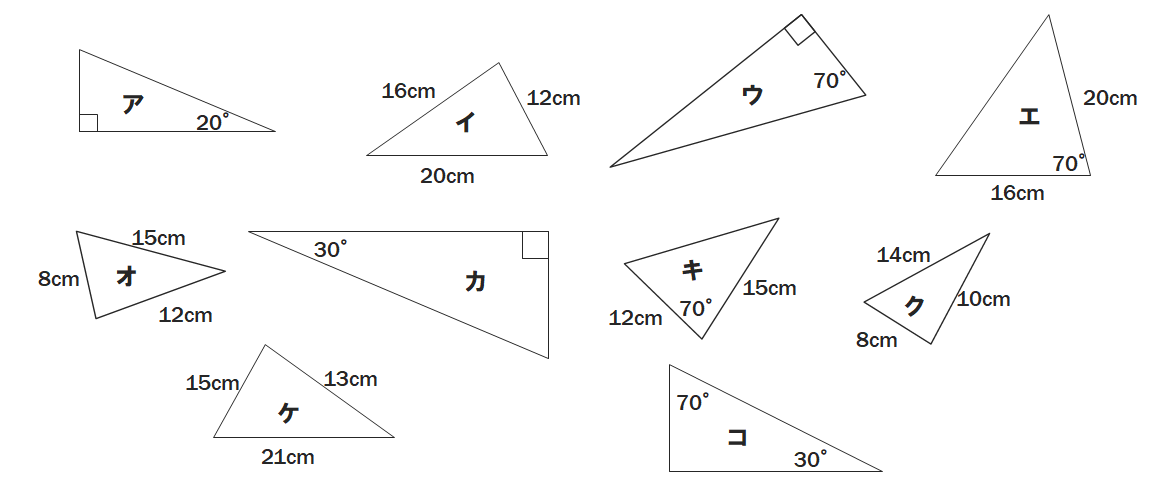



中3数学 相似な図形の線分比の定期テスト対策問題 Examee




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
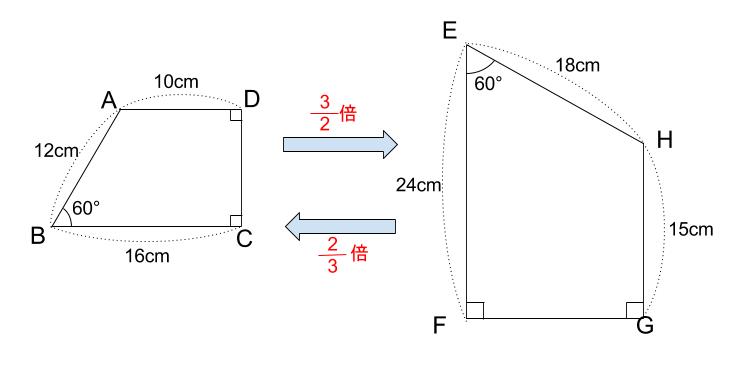



中学数学 相似とは何か 導入 中学数学の無料オンライン学習サイトchu Su




三角形の相似条件と証明問題の解き方 数学fun
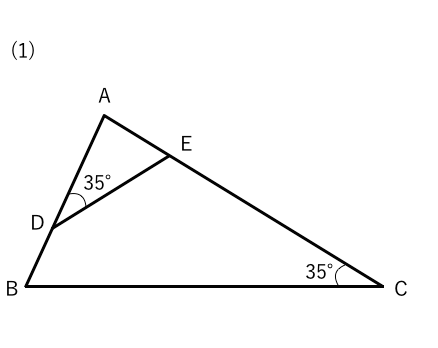



相似な図形 相似条件の練習問題 苦手な数学を簡単に




中3数学 相似な図形 三角形の相似条件を使った証明 2組の角がそれぞれ等しい 三角形の中にある三角形との相似の証明 Youtube
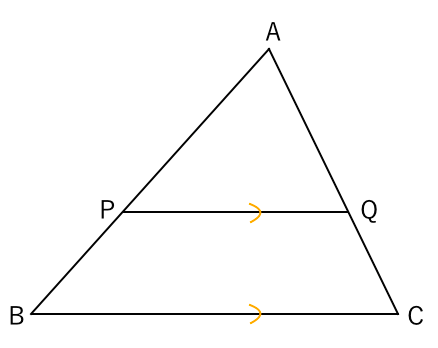



相似な図形 計算について覚えること 苦手な数学を簡単に
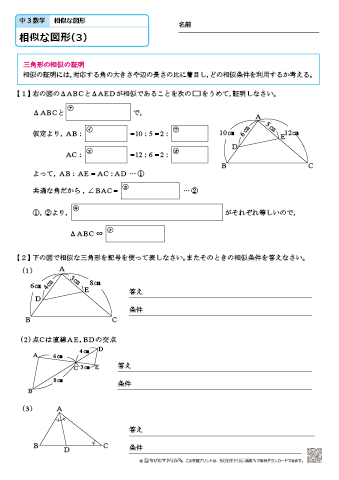



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



1



高校入試数学 相似な三角形の対策問題
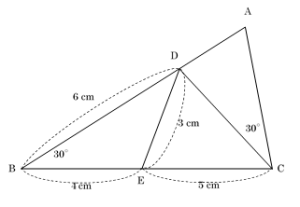



相似な図形 おやじさん ネット




相似な図形 Ict教材eboard イーボード
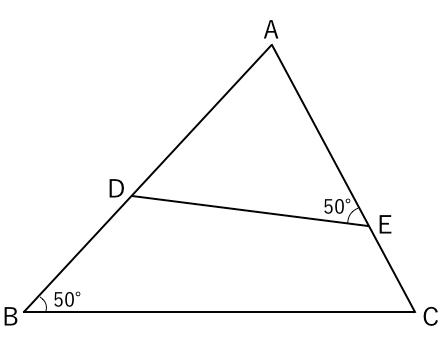



相似 相似な図形を見破れ 苦手な数学を簡単に




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学




三角形の合同条件と証明問題の解き方 数学fun




数学 中3 44 三角形の相似条件 Youtube
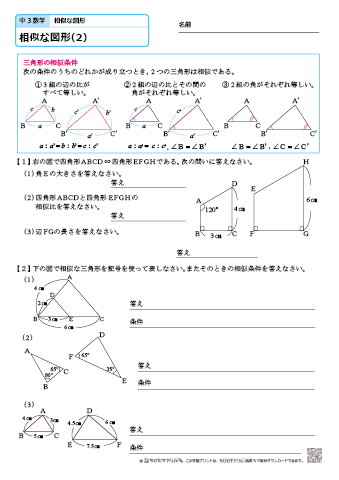



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Airx8l Pcmnnnm



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
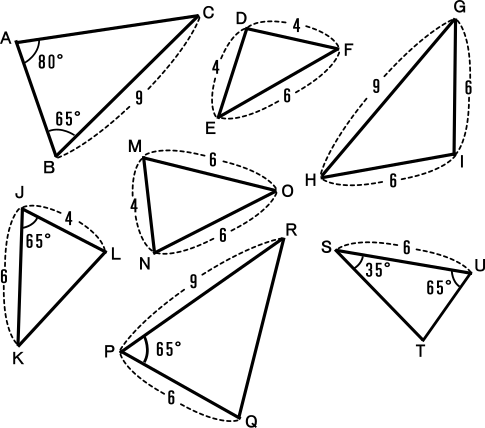



中学3年数学練習問題 三角形の相似条件の問題
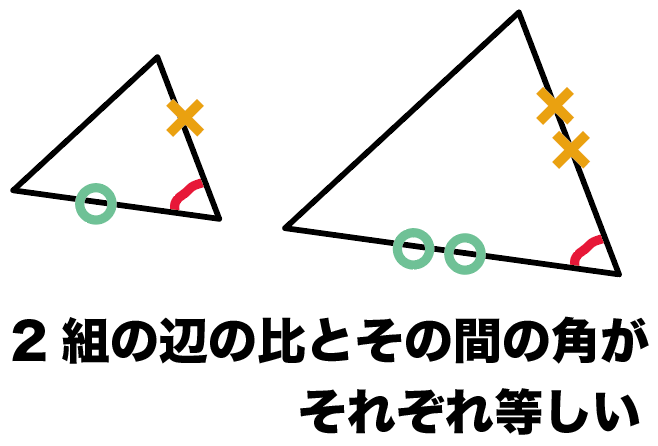



2分でわかる 三角形の3つの相似条件 Qikeru 学びを楽しくわかりやすく



1



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ




Nitter




三角形の相似条件と基本的な証明 無料で使える中学学習プリント



中学数学 三角形の相似条件 中学数学の無料オンライン学習サイトchu Su




中3 中3数学 相似な図形 中学生 数学のノート Clear



合同と相似の複合問題 制限3分 中学数学 理科 寺子屋塾の復習サイト



三角形の相似条件の解説 図形の性質



1




世界一わかりやすい数学問題集中3 5章 図形と相似



中学数学到達度テスト集中3後期 相似な図形 円 三平方の定理 図形と計量 Gakurin1346 学林舎 通販 Yahoo ショッピング




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf



Studydoctor三角形の相似条件 中3数学 Studydoctor




三角形の相似条件と証明問題の解き方 数学fun




相似な図形と三角形の相似条件 まぜこぜ情報局



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




図形の相似 Wikipedia
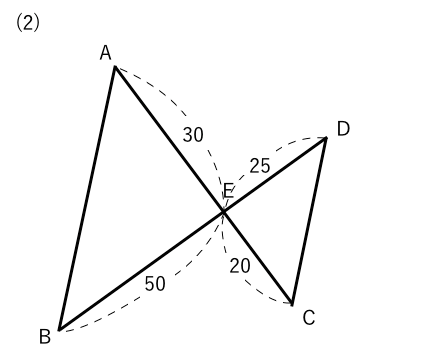



相似な図形 相似条件の練習問題 苦手な数学を簡単に



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
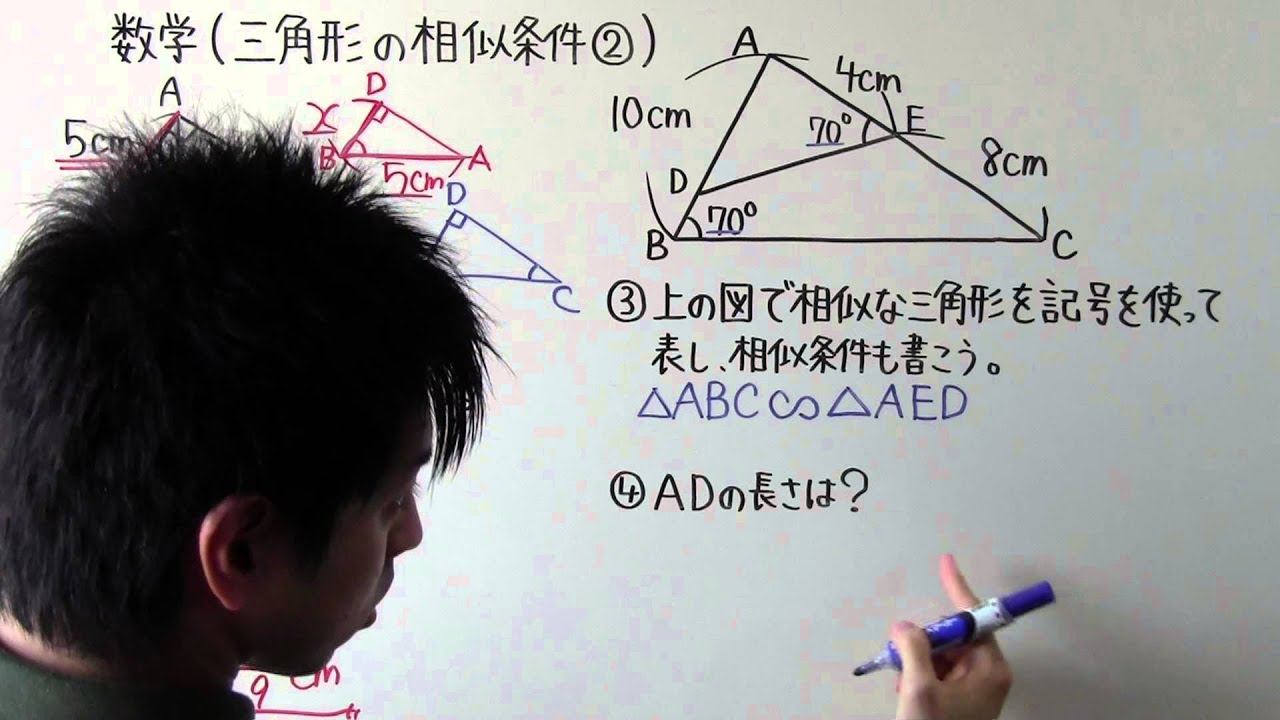



数学 中3 45 三角形の相似条件 Youtube



相似な図形 Ict教材eboard イーボード




無料 中3数学 標準問題 解答プリント 327 図形の相似2 相似条件と証明




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題



本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download
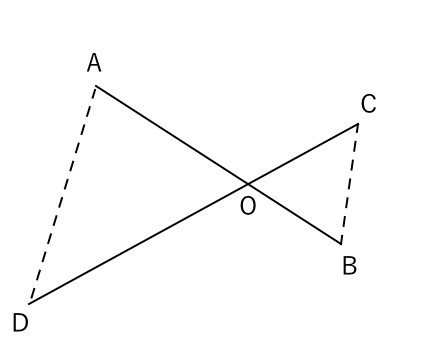



相似な図形 証明に慣れよう 苦手な数学を簡単に




無料 中3数学 基本解説 解答プリント 327 図形の相似2 相似条件と証明
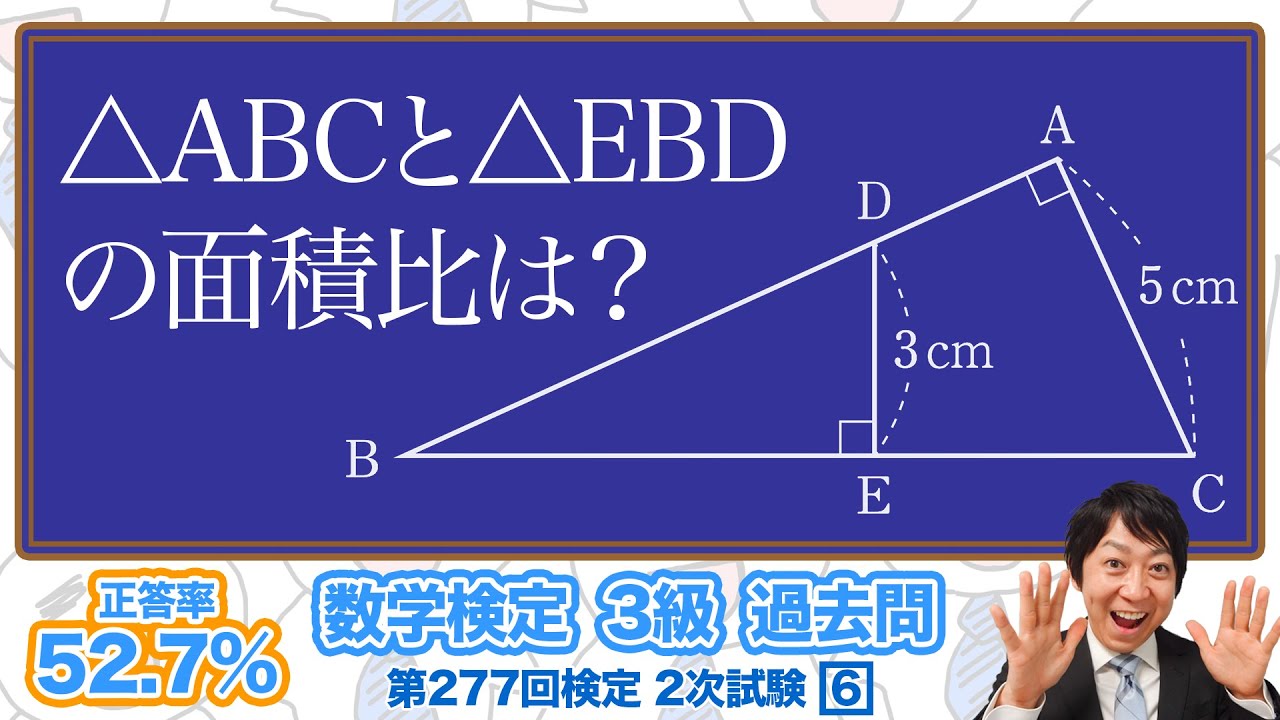



数学検定1級合格者が解説 相似な図形の面積比 合同条件と相似条件の確認 3級 277回 2次 6 数検3級 Youtube



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



相似な図形 三角形の相似条件 相似比 勉強ナビゲーター




相似な図形 Ict教材eboard イーボード




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿