円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h数学的な考え方 角柱や円柱の体積の求め方を既習の立体の体積の求め方に帰着して考え, 説明することができる。 数量や図形についての 技能 公式を用いて角柱や円柱の体積を求めることができる。 数量や図形についての 知識・理解 角柱や円柱の体積の求め方及び公式について理解する。 4 立体の表面積の求め方や公式をまとめましたが、基本にのっとって丁寧に計算するもよし、公式に当てはめて求めてもよしです。また表面積だけでなく、体積を求める問題とも多く出会うでしょう。問題演習の数をこなして、慣れるのを意識してみてください。 *練習問題の回答* (1)a 三

小5 算数 小5 5 体積の求め方のくふう Youtube
立体の体積の求め方 積分
立体の体積の求め方 積分-具体例で学ぶ数学 > 図形 > 三角柱、四角柱、円柱の体積の求め方 最終更新日 三角柱の体積、四角柱の体積、円柱の体積 は全て 底面積×高さ で計算できる。 「柱」と名のつく立体の体積は、全て 底面積×高さ で求めることができます!指導にあたっては,「角柱の体積」では,直方体の求積公式の見直し, 公式の(縦)×(横)は底面に並ぶ 単位立方体の数と底面積を表す個数と等しいことに気づかせるために,底面における1㎤の立体模型の数と紙 の面積の数が等しいことを理解させ,直方体の体積が底面積×高さで考えられるようにする。この求め方を四 角柱や三角柱,さらに円柱にも適応できることに気付かせることから,底面




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
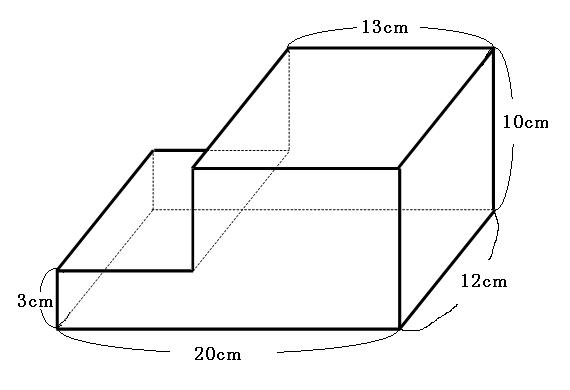
1 単元名 体積の求め方を考えよう(東京書籍 6 年上) 2 単元について (1) 教材について 本単元で扱う角柱と円柱の体積は,学習指導要領には以下のように位置づけられている。 第6 学年「B量と測定」 (3)図形の体積を計算によって求めることができるようにする。 ア 角柱及び円柱の体積の立方体の12の辺の長さは等しく、これを a a とします。 立方体の体積 V V は、次の式で求められます。 《立体の体積の求め方》 求める立体は①と②があわさって出来た立体であることから、①の直方体の体積+②の立方体の体積で求めることが出来ます。 ①の直方体の体積=8×8×4=256(cm³) ②の立方体の体積=4×4×4=64(cm³)
・ 円周 = 直径 × 314 (π) ・ 側面積 = 底面の周 × 高さ ・ 円の面積 = 半径 × 半径 × 314 (π)動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru次の立体の体積を求めましょう 問題① 底面の形は五角形です 底面を3つの三角形にわけて面積を求めます アの面積 10×3÷2=15 イの面積 10×5÷2=25 ウの面積 8×3÷2=12 合計すると 15+25+12=52 体積は 底面積×高さ だから 52×7=364 答え 364
そうすると、例題の直方体の場合、縦・横に 3 3 個・ 4 4 個と並べているので 1 1 段に 12 12 個。 これを 5 5 段並べているので 12× 5=60 12 × 5 = 60 個だとわかります。 1cm3 1 c m 3 が 60 60 個なので、体積は 60cm3 60 c m 3 です。 という求め方になります。 いずれにしても、横になってても柱というポイントを押さえましょう。 高さを求める問題 例題2)下の図のように、底面の半径が2cm、体積が24 \(\pi\) ㎤の円柱があります。この円柱の高さを求めなさい。 19 北海道公立高校入試問題 24 この例題2のような高求め方を利用して U字型の立体の体積につい て多様な求め方を考え、やり やすい方法で計算する ICT 活用環境等 使用周辺機器 プロジェクター 使用ソフト Microsoft PowerPoint 使用教室 コンピュータ教室 成果と課題 授業後に意識調査・客観テスト・面接にてICT を利用していないグ ループとの比較
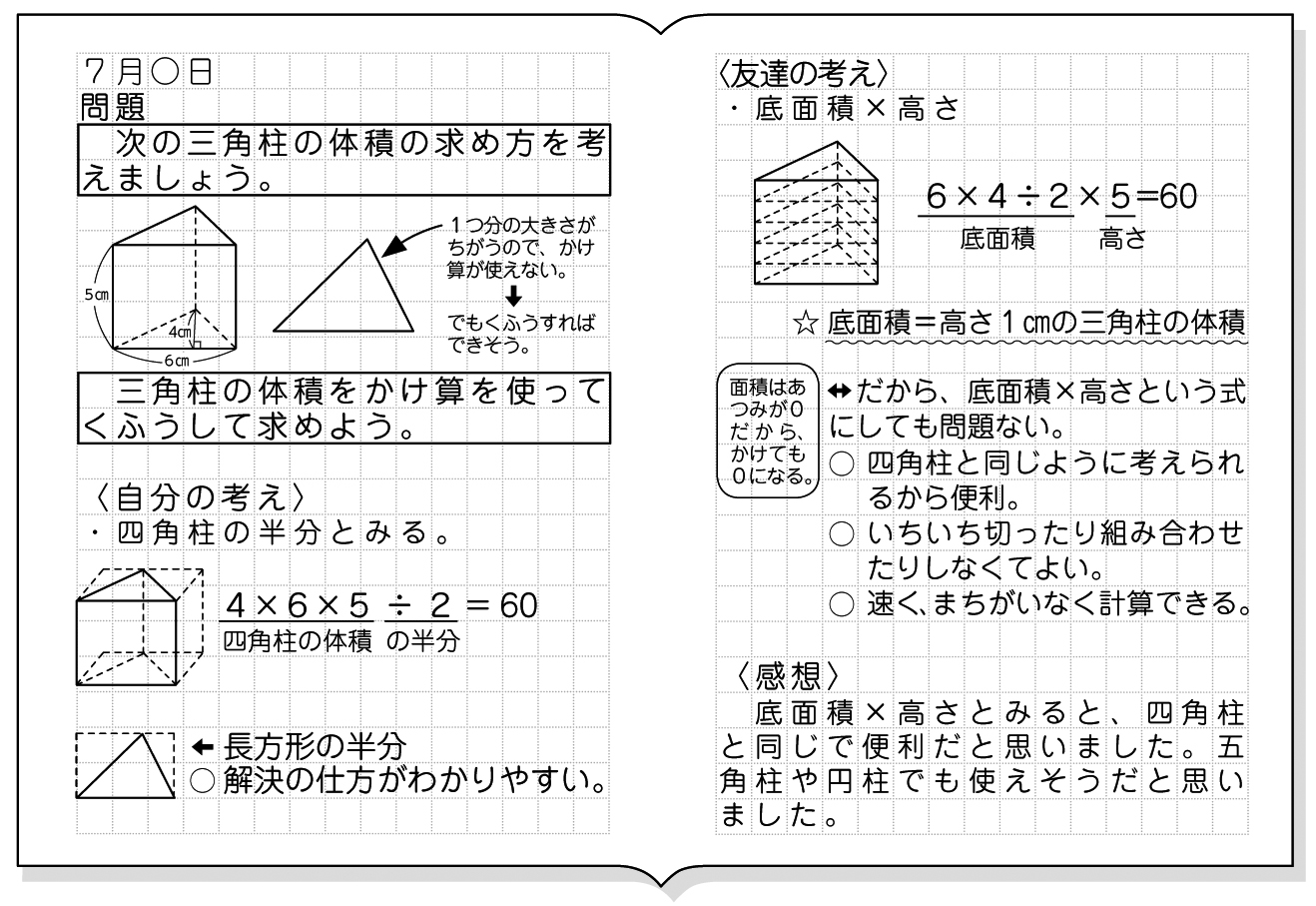



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術




丸棒の重量 円柱の体積と重量の求め方 鉄の場合
正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて複合図形の体積の求め方を、既習の求積方法をもとに考え、説明で きる。図や式を読み取り共有する中で、多様な求積方法を理解でき る。 2 体積 実践ガイド 小学校 算数 5年生 「体積をくふうして求めよう(L字型1)」 単元名 東京書籍 ねらい 複合図形の体積の学習時 実施場面 活 動 の7 立体の体積と表面積 学基本学習の基本 37 切断と体積⑴ 問題 右の図は ,ab = 6 cmad ae 3 の直方体で ある。辺 ad の中点を m ,辺 bc の中点を n とし,この直方体を 次の平面で切るとき,頂点 a をふくむ方の立体の体積を求めよ。 ⑴ 3 点 m ,n,e を通る平面




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座
四角錐台の体積 110 /191件 表示件数 5 10 30 50 100 0 1 01 40歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 建築設計の折り上げ天井の空調気積と平均天井高さ ご意見・ご感想 計算式も提示頂いてるので、根拠を示せるので助かりました。体積ボタン2 解説 立体(L字型) 解説 6年 分数のかけ算とわり算 解説 図形・円と直線の関係 解説 比例 解説 比例と反比例① 解説 比例と反比例① v2 解説 比例と反比例② 解説 変化する2つの量 解説 割合を使って 解説 備蓄計画 解説 比とその利用 味見ロボット「OK」くん 解説 積分計算による体積の求め方! 断面積の積分や回転体の体積 21年2月19日 この記事では、「立体の体積を積分計算で求める方法」についてわかりやすく解説していきます。 各種公式や問題の解き方なども説明していくので、ぜひこの記事を通して




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ
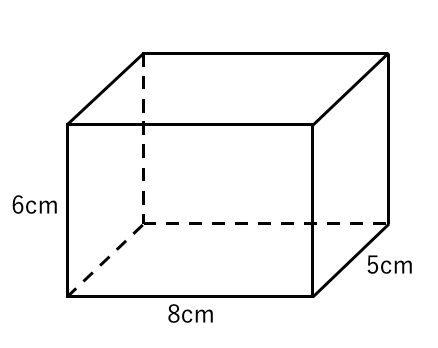
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にしてLesson 43 立体の体積 第6章 空間図形 1 右図の四角柱の体積を求めなさい。 =192 ≪答≫ 体積:192cm 3 2 右図の三角柱の体積を求めなさい。 =72 ≪答≫ 体積:72cm 3 3 右図の円柱の体積を求めなさい。 2 =2π ≪答≫ 体積:2πcm 3 練習問題2 以下の問いに答えなさい。 1 右図の立体の体積の単位や体積の求め方について,数学的に表現・処理したことを振り返り,多面的にと らえ検討してよりよいものを求めて粘り強く考えたり,数学のよさに気付き学習したことを今後の 生活や学習に活用しようとしたりしている。 学びに向かう力,人間性等 学級 個 (3)児童観 (4




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント



立体の体積を求める 苦手な数学を簡単に
体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。 立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle 答え)体積26 cm 3 表面積cm 2 積み重ねられた立体の表面積:(前+右+上)×2 積み重ねられた立体①:表面積と体積! 答え)体積640cm 3 表面積480cm 2 上記のようにある程度、自分の頭で「投影図→見取り図」が




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか
立体の体積の求め方 これで,円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが,以上の議論は,「任意の立体について,基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば,その立体の体積を定積分により求めることができる。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。 たとえば、半径30 cmのサッカーボールがあったとしよう立体の体積の基本的な求め方の練習と、いくつかの直方体・立方体が組み合わさった立体の体積を求める考え方を練習します。 体積(直方体・立方体)(1) 答え 体積(直方体・立方体)(2) 答え 体積(直方体・立方体)(3) 答え 体積(直方体




体積の求め方 公式一覧 小学生 中学生の勉強




小5 算数 小5 5 体積の求め方のくふう Youtube
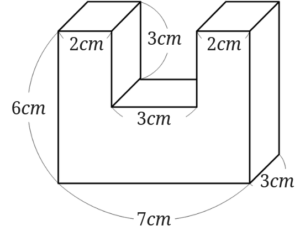
・立方体,直角柱の体積の求め方 6年生 ・角柱,円柱の体積の求め方 表1 表1を見ると,平面図形の四角形の学習では, はじめに,辺が垂直に交わる正方形や長方形を学 習する。次に,辺が直交しない四角形として平行 四辺形を学習している。立体においてその他の立体図形の体積の算定は下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 実際に、下図の立方体の体積を求めましょう。 例えば立方体の体積=m 3 のとき1辺の長さは約27mです。 立方体の値とリットルの関係 立方体の体積が1立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も(A)のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



1
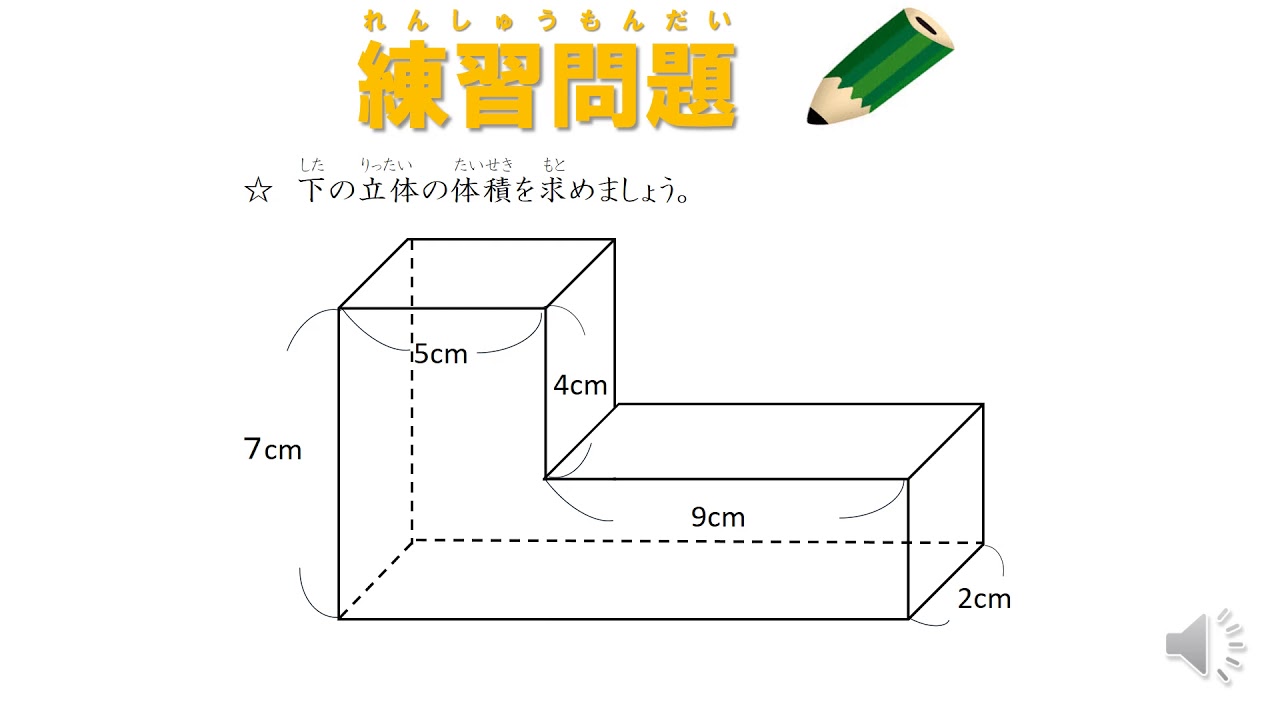
小学5年生の算数 体積 立体の体積の求め方 練習プリント 小学5年生の算数立体の体積の求め方練習プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 小学5年生の算数直方体と立方体を組み合わせ複合図形の体積の求め方 図形を分けたり、合わせたりして自分の知っている形にする。 5㎝ 4㎝ 9㎝ 5㎝ 4㎝ 3㎝ 9 ㎝ 四角柱の底面の形に注目してみると cm 、下底9 、高さ3 平面の台形を高さ4 cm まで積み上げたと考えると の体積=底面積×高さ;V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロン




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
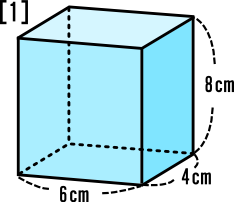
この円柱において, 底面の面積は,π×22=4π(cm2), 高さは 2cm なので, 円柱の体積=底面の面積×高さ より, 体積は,4π×2=8π(cm3)となります。粘土でできた立体の体積の求め方をいろいろ考え出そう。 つぶして直方体(立 方体)にする。 1ℓますに詰めて縦・ 横・高さを調べる。 直方体と捉 えて縦横・高 さを概測し て計算する。 1㎤の何個分 か調べる。 1㎤と全体 の重さから 計算する。 水に沈めて増えた 水かさを調べる。 水が満タン問2 ADE を,直線 AD を軸として1回転してできる立体の体積を求めなさい。 (鳥取県15年入試問題) 解説 やり直す (cm 3) (cm 3) (cm 3) (cm 3) 問題62 右の図Ⅰのように, AC=6 cm , BC=8 cm , AD=5 cm , ∠ACB=90° の三角柱がある。このとき,次の各問いに答えなさい。 問1,問3 略 問2 ADE を,直線 AD を




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




角柱 円柱の表面積と体積の公式 数学fun
本単元で扱う立体の体積の求め方は,学習指導要領には以下のように位置づけられている。 第6学年 b 量と測定 (3)図形の体積を計算によって求めることができるようにする。 ア 角柱および円柱の体積の求め方を考えること。方 1 三角柱の体積を計算で求める方法を 理解する。 既習の立体の体積の求め方を手がかりに、角 柱の体積の求め方を見直す。 *底面が直角三角形の三角柱の体積も、底面積 ×高さで求められることを考える。 2 一般の角柱の体積の公式をまとめ る。の体積を 求めなさい。 ア イ ウ エ 解説 ア 6×8÷2×7=168cm 3 。 イ 2×2×314×6=7536cm 3 。 ウ 6×8×7× 1 3 =112cm 3 。 エ 2×2×314×6× 1 3 =2512cm 3 。 解答 ア168cm 3 イ7536cm 3 ウ112cm 3 エ2512cm 3 例題2 右の図は直方体から立方体を切り取ったものです。 立体の体積と表面積を求め




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




この立体の体積の求め方が分かりません Clear



1




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




立体の表面積 小学生算数です教えて下さい Okwave



6年算数立体の体積1 教え方




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




四角錐台の体積 高精度計算サイト



立体の表面積




円柱の表面積と体積を求める公式 具体例で学ぶ数学



三角柱の体積を求める時にテキストでは2分の1と出ているんですがこれは何なんで Yahoo 知恵袋



6年算数立体の体積その2 教え方




小5 複雑な立体の体積 直方体 日本語版 Youtube




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット



中学1年数学練習問題 立体 円錘 三角錘等 の表面積の求め方と解答



三角錐の体積の求め方 下の図は立方体から三角錐を切り取った立 Yahoo 知恵袋




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




6年算数立体の体積1 教え方



5 5 複雑な立体の表面積と面積を求めるには さんすうがく



立派な 台形 体積 求め 方




立体の体積を求める公式




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
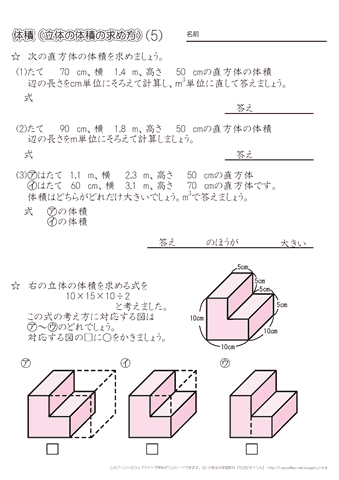



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
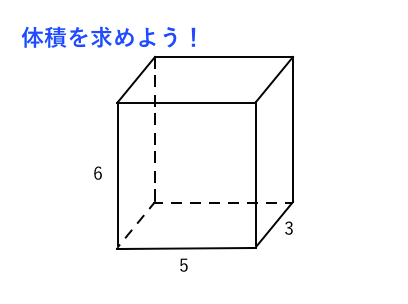



超簡単 体積の求め方 苦手な数学を簡単に




体積の求め方 計算公式一覧




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor



6 3 複雑な図形を1回転させてできる立体の体積と表面積を求めるには さんすうがく パート 2
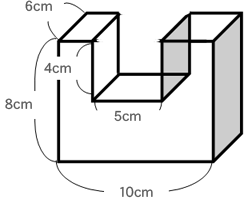



体積 直方体と立方体のかさを表そう 第5学年 小学校 算数 My実践事例 日本文教出版
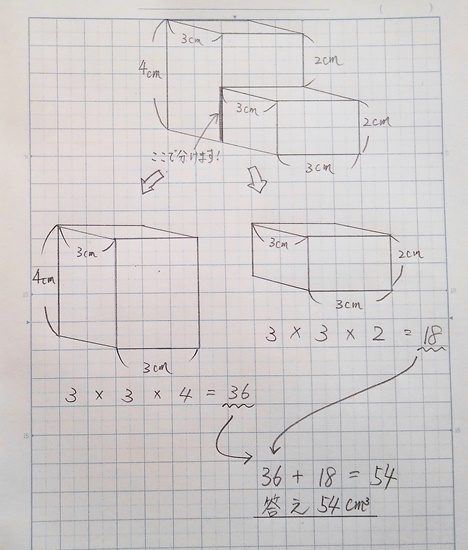



5年生 算数 体積の勉強 小学生の勉強法 親子学びスクール




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




角柱の体積 Youtube




体積 表面積




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校



写真の底面が扇形の立体の表面積の求め方を教えてください 特に側面積が Yahoo 知恵袋




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



1



小5 直方体の体積 複雑な立体を求める 日本語版 Youtube
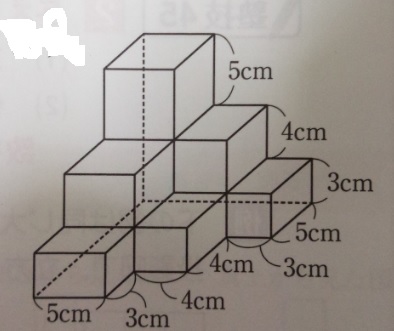



積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法




スタディピア 立体の体積




小5 算数 小5 3 直方体と立方体の体積 Youtube



5年算数体積2わかる教え方
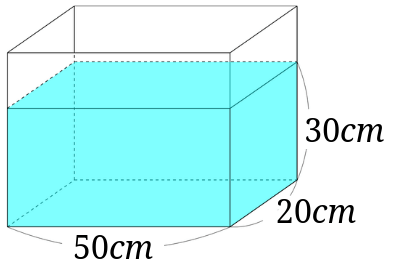



石を水の入った水槽に沈めて体積を求める問題の教え方 みけねこ小学校




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




2 を途中式を含めて教えてください Clear




Pin On Matematicas




体積の求め方 計算公式一覧




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
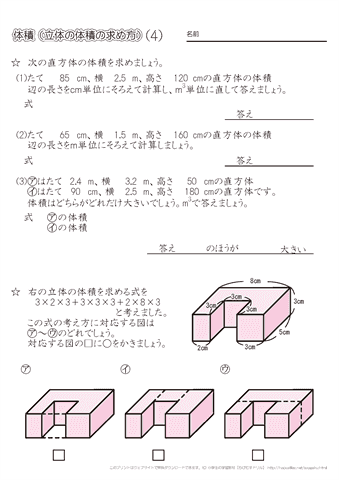



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
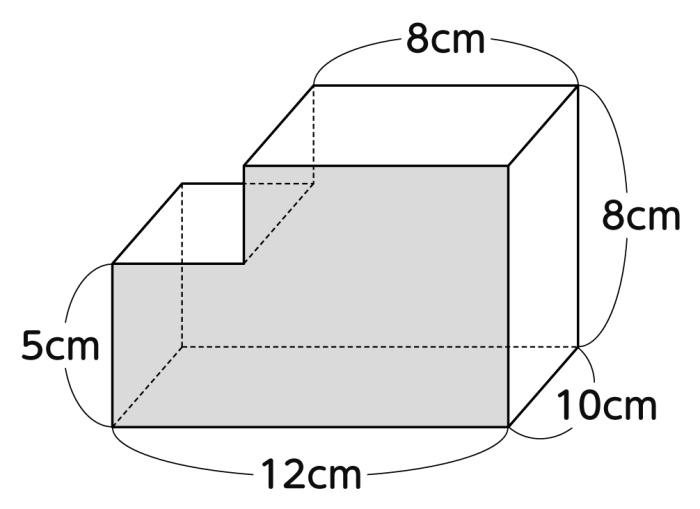



動画で学習 1 角柱と円柱の体積 算数




体積の求め方 計算公式一覧




6年算数 立体の体積 のわかる教え方 いっちに算数 のブログ




公式を図解 すい体の体積 円すいの表面積の求め方




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
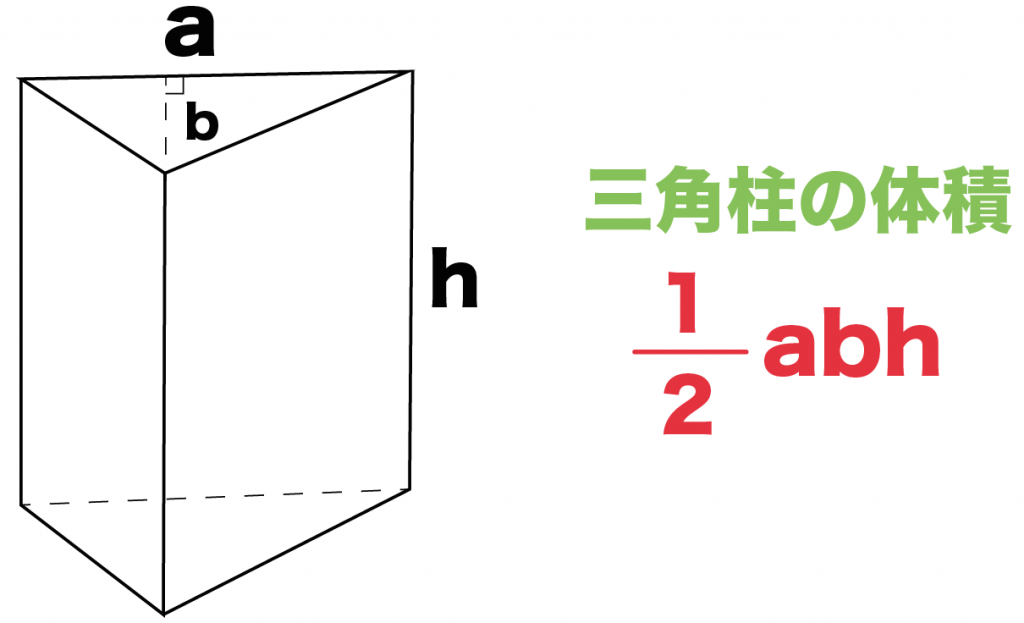



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




体積の求め方 計算公式一覧




角錐 円錐の体積と表面積の公式 数学fun




球の表面積と体積の公式 数学fun




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



Q Tbn And9gcqbxowgsr9fglz9s6nk3xfp1u T2gn5wllytdkpbbfnrgtv43gf Usqp Cau




体積の求め方 公式一覧 小学生 中学生の勉強




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



立体 の 表面積 求め 方



0 件のコメント:
コメントを投稿